搜索
【题目】设函数 
．
（1）当a=b=2时，证明：函数f（x）不是奇函数；
（2）设函数f（x）是奇函数，求a与b的值；
（3）在（2）条件下，判断并证明函数f（x）的单调性，并求不等式 
的解集．
参考答案：
【答案】
（1）解：当a=b=2时， 
，
∵ 
，f（1）=0，
∴f（﹣1）≠﹣f（1），
∴函数f（x）不是奇函数
（2）解：由函数f（x）是奇函数，得f（﹣x）=﹣f（x），
即 
对定义域内任意实数x都成立，
整理得（2a﹣b）22x+（2ab﹣4）2x+（2a﹣b）=0对定义域内任意实数x都成立，
∴ 
，
解得 
或 
经检验 符合题意
（3）解：由（2）可知 
易判断f（x）为R上的减函数，
证明：∵2x+1在定义域R上单调递增且2x+1＞0，
∴ 
在定义域R上单调递减，且 ＞0，
∴ 在R上单调递减．
由 
，不等式 
，
等价为f（x）＞f（1），
由f（x）在R上的减函数可得x＜1．
另解：由 得，即 
，
解得2x＜2，∴x＜1．
即不等式的解集为（﹣∞，1）
【解析】（1）根据函数奇偶性的定义进行判断函数f（x）不是奇函数；（2）根据奇函数的性质建立方程即可求a与b的值；（3）根据函数单调性的定义或性质证明函数f（x）的单调性，并利用单调性的性质解不等式 ．
【考点精析】利用函数单调性的性质和函数的奇偶性对题目进行判断即可得到答案，需要熟知函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集；偶函数的图象关于y轴对称；奇函数的图象关于原点对称．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）=log4（2x+3﹣x2）．
（1）求f（x）的定义域及单调区间；
（2）求f（x）的最大值，并求出取得最大值时x的值；
（3）设函数g（x）=log4[（a+2）x+4]，若不等式f（x）≤g（x）在x∈（0，3）上恒成立，求实数a的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】现有
（n≥2，n∈N*）个给定的不同的数随机排成一个下图所示的三角形数阵：
设Mk是第k行中的最大数，其中1≤k≤n，k∈N*．记M1＜M2＜…＜Mn的概率为pn．
（1）求p2的值；
（2）证明：pn＞
． -
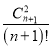科目： 来源： 题型：
查看答案和解析>>【题目】已知：全集U=R，函数
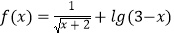的定义域为集合A，集合B={x|x2﹣a＜0}
（1）求UA；
（2）若A∪B=A，求实数a的范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f (x)＝ex－ax－1，其中e为自然对数的底数，a∈R．
（1）若a＝e，函数g (x)＝(2－e)x．
①求函数h(x)＝f (x)－g (x)的单调区间；
②若函数
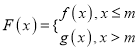的值域为R，求实数m的取值范围；（2）若存在实数x1，x2∈[0，2]，使得f(x1)＝f(x2)，且|x1－x2|≥1，
求证：e－1≤a≤e2－e．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）=
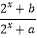（a、b为常数），且f（1）= 
，f（0）=0．
（1）求函数f（x）的解析式；
（2）判断函数f（x）在定义域上的奇偶性，并证明；
（3）对于任意的x∈[0，2]，f（x）（2x+1）＜m4x恒成立，求实数m的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）=x2+mx﹣4在区间[﹣2，1]上的两个端点处取得最大值和最小值．
（1）求实数m的所有取值组成的集合A；
（2）试写出f（x）在区间[﹣2，1]上的最大值g（m）；
（3）设h（x）=﹣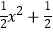
x+7，令F（m）= 
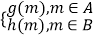，其中B=RA，若关于m的方程F（m）=a恰有两个不相等的实数根，求实数a的取值范围．
相关试题
