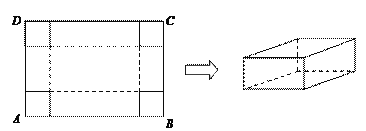
【题目】在一张足够大的纸板上截取一个面积为3600平方厘米的矩形纸板ABCD,然后在矩形纸板的四个角上切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸盒(如图).设小正方形边长为x厘米,矩形纸板的两边AB,BC的长分别为a厘米和b厘米,其中a≥b.
(1)当a=90时,求纸盒侧面积的最大值;
(2)试确定a,b,x的值,使得纸盒的体积最大,并求出最大值.
参考答案:
【答案】(1)当x=![]() 时,纸盒的侧面积的最大值为
时,纸盒的侧面积的最大值为![]() 平方厘米;
平方厘米;
(2)当a=b=60,x=10时纸盒的体积最大,最大值为16000立方厘米.
【解析】试题分析:(1)矩形纸板![]() 的面积为
的面积为![]() ,故当
,故当![]() 时,
时, ![]() ,列出关于纸盒侧面积
,列出关于纸盒侧面积![]() 函数解析式,利用二次函数的性质,即可求得最大值;
函数解析式,利用二次函数的性质,即可求得最大值;
(2)列出盒子体积![]() 的函数解析式,利用导数求解函数的单调性、最值,即可得到结论。
的函数解析式,利用导数求解函数的单调性、最值,即可得到结论。
试题解析:
(1)因为矩形纸板ABCD的面积为3600,故当a=90时,b=40,
从而包装盒子的侧面积
S=2×x(90-2x)+2×x(40-2x)
=-8x2+260x,x∈(0,20) .
因为S=-8x2+260x=-8(x-![]() )2+
)2+![]() ,
,
故当x=![]() 时,侧面积最大,最大值为
时,侧面积最大,最大值为 ![]() 平方厘米.
平方厘米.
答:当x=![]() 时,纸盒的侧面积的最大值为
时,纸盒的侧面积的最大值为![]() 平方厘米.
平方厘米.
(2)包装盒子的体积
V=(a-2x)(b-2x) x=x[ab-2(a+b)x+4x2],x∈(0,),b≤60.
V=x[ab-2(a+b)x+4x2]≤x(ab-4![]() x+4x2)
x+4x2)
=x(3600-240x+4x2)
=4x3-240x2+3600x. 当且仅当a=b=60时等号成立.
设f (x)=4x3-240x2+3600x,x∈(0,30).
则f ′ (x)=12(x-10)(x-30).
于是当0<x<10时,f ′ (x)>0,所以f (x)在(0,10)上单调递增;
当10<x<30时,f ′ (x)<0,所以f (x)在(10,30)上单调递减.
因此当x=10时,f (x)有最大值f (10)=16000, 此时a=b=60,x=10.
答:当a=b=60,x=10时纸盒的体积最大,最大值为16000立方厘米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
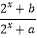 (a、b为常数),且f(1)=
(a、b为常数),且f(1)=  ,f(0)=0.
,f(0)=0.
(1)求函数f(x)的解析式;
(2)判断函数f(x)在定义域上的奇偶性,并证明;
(3)对于任意的x∈[0,2],f(x)(2x+1)<m4x恒成立,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2+mx﹣4在区间[﹣2,1]上的两个端点处取得最大值和最小值.
(1)求实数m的所有取值组成的集合A;
(2)试写出f(x)在区间[﹣2,1]上的最大值g(m);
(3)设h(x)=﹣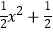 x+7,令F(m)=
x+7,令F(m)= 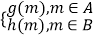 ,其中B=RA,若关于m的方程F(m)=a恰有两个不相等的实数根,求实数a的取值范围.
,其中B=RA,若关于m的方程F(m)=a恰有两个不相等的实数根,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,焦点在x轴上的椭圆C:
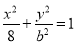 经过点(b,2e),其中e为椭圆C的离心率.过点T(1,0)作斜率为k(k>0)的直线l交椭圆C于A,B两点(A在x轴下方).
经过点(b,2e),其中e为椭圆C的离心率.过点T(1,0)作斜率为k(k>0)的直线l交椭圆C于A,B两点(A在x轴下方).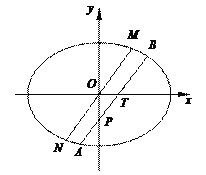
(1)求椭圆C的标准方程;
(2)过点O且平行于l的直线交椭圆C于点M,N,求
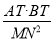 的值;
的值;(3)记直线l与y轴的交点为P.若
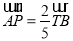 ,求直线l的斜率k.
,求直线l的斜率k. -
科目: 来源: 题型:
查看答案和解析>>【题目】某赛季,甲、乙两名篮球运动员都参加了11场比赛,他们每场比赛得分的情况用如图所示的茎叶图表示,则甲、乙两名运动员的中位数分别为( )
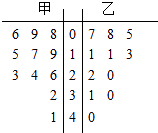
A.19、13
B.13、19
C.20、18
D.18、20 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥P-ABCD中,AD⊥平面PAB,AP⊥AB.
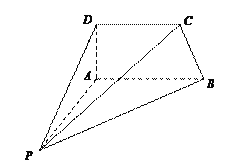
(1)求证:CD⊥AP;
(2)若CD⊥PD,求证:CD∥平面PAB;
-
科目: 来源: 题型:
查看答案和解析>>【题目】设P和0是两个集合,定义集合PQ={x|x∈P,且x≠Q},如果P={x|log2x<1},Q={x||x﹣2|<1},那么PQ等于 .
相关试题

