【题目】已知焦点在![]() 轴上的椭圆
轴上的椭圆![]() 的中心是原点
的中心是原点![]() ,离心率为双曲线
,离心率为双曲线![]() 离心率的一半,直线
离心率的一半,直线![]() 被椭圆
被椭圆![]() 截得的线段长为
截得的线段长为![]() .直线
.直线![]() :
: ![]() 与
与![]() 轴交于点
轴交于点![]() ,与椭圆
,与椭圆![]() 交于
交于![]() 两个相异点,且
两个相异点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在实数![]() ,使
,使![]() ?若存在,求
?若存在,求![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
参考答案:
【答案】(Ⅰ) ![]() ;(Ⅱ)
;(Ⅱ) ![]() 或
或![]() 或
或![]() .
.
【解析】试题分析:(Ⅰ)设出椭圆的标准方程,利用离心率、四边形的周长进行求解;(Ⅱ)利用平面向量的线性运算得到![]() 的关系,联立直线与椭圆的方程,得到关于
的关系,联立直线与椭圆的方程,得到关于![]() 的一元二次方程,利用椭圆的对称性、平面向量的坐标运算和判别式进行求解.
的一元二次方程,利用椭圆的对称性、平面向量的坐标运算和判别式进行求解.
试题解析:(Ⅰ)根据已知设椭圆![]() 的方程为
的方程为![]() ,焦距为
,焦距为![]() ,
,
由已知得![]() ,∴
,∴![]() .
.
∵以椭圆![]() 的长轴和短轴为对角线的四边形的周长为
的长轴和短轴为对角线的四边形的周长为![]() ,
,
∴![]() .
.
∴椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)根据已知得![]() ,由
,由![]() ,得
,得![]() .
.
∴![]() .∵
.∵![]() ,∴
,∴![]() ,
,
若![]() ,由椭圆的对称性得
,由椭圆的对称性得![]() ,即
,即![]() .
.
∴![]() 能使
能使![]() 成立.
成立.
若![]() ,则
,则![]() ,解得
,解得![]() .
.
设![]() ,由
,由![]() 得
得![]() ,
,
由已知得![]() ,即
,即![]() .
.
且![]() .…10分
.…10分
由![]() 得
得![]() ,即
,即![]() .∴
.∴![]() ,
,
∴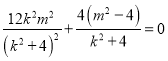 ,即
,即![]() .
.
当![]() 时,
时, ![]() 不成立.∴
不成立.∴![]() ,
,
∵![]() ,∴
,∴![]() ,即
,即![]() .
.
∴![]() ,解得
,解得![]() 或
或![]() .
.
综上述,当![]() 或
或![]() 或
或![]() 时,
时, ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若函数f(x)在定义域上存在区间[a,b](ab>0),使f(x)在[a,b]上值域为[
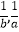 ],则称f(x)在[a,b]上具有“反衬性”.下列函数①f(x)=﹣x+
],则称f(x)在[a,b]上具有“反衬性”.下列函数①f(x)=﹣x+  ②f(x)=﹣x2+4x ③f(x)=sin
②f(x)=﹣x2+4x ③f(x)=sin  x ④f(x)=
x ④f(x)= 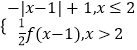 ,具有“反衬性”的为|( )
,具有“反衬性”的为|( )
A.②③
B.①③
C.①④
D.②④ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=1,AD=
 ,P矩形内的一点,且AP=
,P矩形内的一点,且AP= 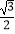 ,若
,若 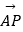 =λ
=λ 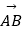 +μ
+μ 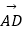 ,(λ,μ∈R),則λ+
,(λ,μ∈R),則λ+  μ的最大值为 .
μ的最大值为 . 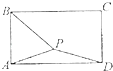
-
科目: 来源: 题型:
查看答案和解析>>【题目】给定两个命题,P:对任意实数x都有ax2+ax+1>0恒成立;Q:关于x的方程x2﹣x+a=0有实数根;如果P与Q中有且仅有一个为真命题,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2﹣mx+1﹣m2 , 若|f(x)|在[0,1]上单调递增,则实数m的取值范围 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC三个顶点坐标分别为:A(1,0),B(1,4),C(3,2),直线l经过点(0,4).
(1)求△ABC外接圆⊙M的方程;
(2)若直线l与⊙M相交于P,Q两点,且|PQ|=2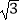 ,求直线l的方程.
,求直线l的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2﹣lnx.
(1)求曲线f(x)在点(1,f(1))处的切线方程;
(2)求函数f(x)的单调递减区间:
(3)设函数g(x)=f(x)﹣x2+ax,a>0,若x∈(O,e]时,g(x)的最小值是3,求实数a的值.(e为自然对数的底数)
相关试题

