【题目】若函数f(x)在定义域上存在区间[a,b](ab>0),使f(x)在[a,b]上值域为[ ![]() ],则称f(x)在[a,b]上具有“反衬性”.下列函数①f(x)=﹣x+
],则称f(x)在[a,b]上具有“反衬性”.下列函数①f(x)=﹣x+ ![]() ②f(x)=﹣x2+4x ③f(x)=sin
②f(x)=﹣x2+4x ③f(x)=sin ![]() x ④f(x)=
x ④f(x)= 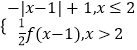 ,具有“反衬性”的为|( )
,具有“反衬性”的为|( )
A.②③
B.①③
C.①④
D.②④
参考答案:
【答案】B
【解析】解:若函数f(x)在定义域上存在区间[a,b](ab>0),使f(x)在[a,b]上值域为[ ![]() ],则等价为函数f(x)与y=
],则等价为函数f(x)与y= ![]() 有两个交点,且函数在区间上单调递减即可.
有两个交点,且函数在区间上单调递减即可.
①若f(x)=﹣x+ ![]() ,作出函数f(x)与y=
,作出函数f(x)与y= ![]() 的图象,由图象知两个函数有两个交点,则f(x)具有“反衬性”,
的图象,由图象知两个函数有两个交点,则f(x)具有“反衬性”,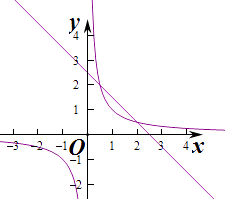
②若f(x)=﹣x2+4x,作出函数f(x)与y= ![]() 的图象,由图象知两个函数有两个交点,但函数在交点对应的区间上不具单调性,则f(x)不具有“反衬性”,
的图象,由图象知两个函数有两个交点,但函数在交点对应的区间上不具单调性,则f(x)不具有“反衬性”,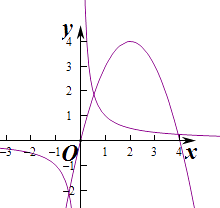
③f(x)=sin ![]() x,作出函数f(x)与y=
x,作出函数f(x)与y= ![]() 的图象,由图象知两个函数有两个交点,函数在交点对应的区间上单调递减,则f(x)具有“反衬性”,
的图象,由图象知两个函数有两个交点,函数在交点对应的区间上单调递减,则f(x)具有“反衬性”,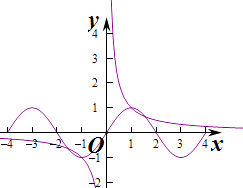
④f(x)= 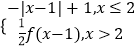 ,
,
当2<x<3时,f(x)= ![]() f(x﹣1)=
f(x﹣1)= ![]() [﹣|x﹣2|+1]=﹣
[﹣|x﹣2|+1]=﹣ ![]() |x﹣2|+
|x﹣2|+ ![]() ,
,
当3<x<4时,f(x)= ![]() f(x﹣1)=
f(x﹣1)= ![]() [﹣
[﹣ ![]() |x﹣3|+
|x﹣3|+ ![]() ]=﹣
]=﹣ ![]() |x﹣2|+
|x﹣2|+ ![]() ,
,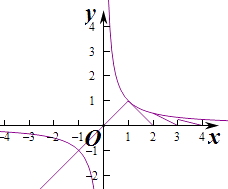
作出函数f(x)与y= ![]() 的图象,由图象知两个函数有两个交点,函数在交点对应的区间上不单调递减,则f(x)不具有“反衬性”,
的图象,由图象知两个函数有两个交点,函数在交点对应的区间上不单调递减,则f(x)不具有“反衬性”,
综上具有“反衬性”的函数是①③,
故选:B
【考点精析】利用函数的定义域及其求法和函数的值域对题目进行判断即可得到答案,需要熟知求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某校组织的“共筑中国梦”竞赛活动中,甲、乙两班各有6名选手参赛,在第一轮笔试环节中,评委将他们的笔试成绩作为样本数据,绘制成如图所示的茎叶图,为了增加结果的神秘感,主持人故意没有给出甲、乙两班最后一位选手的成绩,只是告诉大家,如果某位选手的成绩高于90分(不含90分),则直接“晋级”.
(1)求乙班总分超过甲班的概率;
(2)主持人最后宣布:甲班第六位选手的得分是90分,乙班第六位选手的得分是97分.若主持人从甲乙两班所有选手成绩中分别随机抽取2个,记抽取到“晋级”选手的总人数为
 ,求
,求 的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为倡导全体学生为特困学生捐款,举行“一元钱,一片心,诚信用水”活动,学生在购水处每领取一瓶矿泉水,便自觉向捐款箱中至少投入一元钱.现统计了连续5天的售出和收益情况,如表:
售出水量x(单位:箱)
7
6
6
5
6
收益y(单位:元)
165
142
148
125
150
(1)求y关于x的线性回归方程;
(2)预测售出8箱水的收益是多少元?
附:回归直线的最小二乘法估计公式分别为:
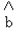 =
=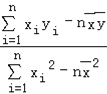 ,
,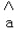 =
= ﹣
﹣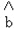
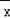 ,
, -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=sin(2ωx+φ)(ω>0,0<φ<π)的最小正周期为π,且函数图象关于点(﹣
 ,0)对称,则函数的解析式为( )
,0)对称,则函数的解析式为( )
A.y=sin(4x+ )
)
B.y=sin(2x+ )
)
C.y=sin(2x+ )
)
D.y=sin(4x+ )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=1,AD=
 ,P矩形内的一点,且AP=
,P矩形内的一点,且AP= 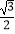 ,若
,若 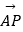 =λ
=λ 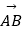 +μ
+μ 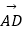 ,(λ,μ∈R),則λ+
,(λ,μ∈R),則λ+  μ的最大值为 .
μ的最大值为 . 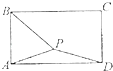
-
科目: 来源: 题型:
查看答案和解析>>【题目】给定两个命题,P:对任意实数x都有ax2+ax+1>0恒成立;Q:关于x的方程x2﹣x+a=0有实数根;如果P与Q中有且仅有一个为真命题,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知焦点在
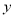 轴上的椭圆
轴上的椭圆 的中心是原点
的中心是原点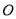 ,离心率为双曲线
,离心率为双曲线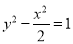 离心率的一半,直线
离心率的一半,直线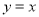 被椭圆
被椭圆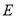 截得的线段长为
截得的线段长为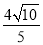 .直线
.直线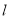 :
: 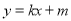 与
与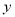 轴交于点
轴交于点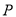 ,与椭圆
,与椭圆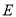 交于
交于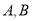 两个相异点,且
两个相异点,且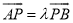 .
.(1)求椭圆
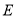 的方程;
的方程;(2)是否存在实数
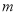 ,使
,使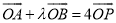 ?若存在,求
?若存在,求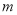 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
相关试题

