【题目】已知△ABC三个顶点坐标分别为:A(1,0),B(1,4),C(3,2),直线l经过点(0,4).
(1)求△ABC外接圆⊙M的方程;
(2)若直线l与⊙M相交于P,Q两点,且|PQ|=2 ![]() ,求直线l的方程.
,求直线l的方程.
参考答案:
【答案】
(1)解:解法1:设⊙M的方程为:x2+y2+Dx+Ey+F=0,
则由题意得 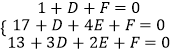 ,解得
,解得 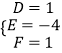 ,
,
∴⊙M的方程为x2+y2﹣2x﹣4y+1=0,或(x﹣1)2+(y﹣2)2=4
解法2:∵A(1,0),B(1,4)的横坐标相同,故可设M(m,2),
由MA2=MC2得(m﹣1)2+4=(m﹣3)2,解得m=1
∴⊙M的方程为(x﹣1)2+(y﹣2)2=4,或x2+y2﹣2x﹣4y+1=0
解法3:∵A(1,0),B(1,4),C(3,2),∴ ![]() ,
,
∴ ![]() ,则△ACB是等腰直角三角形,
,则△ACB是等腰直角三角形,
因而△ACB圆心为(1,2),半径为2,
∴⊙M的方程为(x﹣1)2+(y﹣2)2=4
(2)解:当直线l与x轴垂直时,l方程为x=0,它截⊙M得弦长恰为2 ![]()
当直线l的斜率存在时,设l:y=kx+4
∵圆心到直线y=kx+4的距离d= ![]()
由勾股定理得 ![]() ,解得
,解得 ![]()
故直线l的方程为x=0或3x+4y﹣16=0
【解析】(1)解法1:设⊙M的方程为一般式,根据条件列出方程组,求解后即可求出⊙M的方程;解法2:根据A(1,0),B(1,4)的横坐标相同设M(m,2),由半径相等和两点之间的距离公式列出方程求出m,可得⊙M的方程;解法3:由向量的坐标运算求出 ![]() ,由向量的数量积运算求出
,由向量的数量积运算求出 ![]() 和模,判断出△ACB是等腰直角三角形,由直角三角形外接圆的性质求出⊙M的方程;(2)对直线l的斜率存在问题分类讨论,根据点到直线的距离公式和弦长公式列出方程,求出直线的斜率,即可得到直线方程.
和模,判断出△ACB是等腰直角三角形,由直角三角形外接圆的性质求出⊙M的方程;(2)对直线l的斜率存在问题分类讨论,根据点到直线的距离公式和弦长公式列出方程,求出直线的斜率,即可得到直线方程.
【考点精析】根据题目的已知条件,利用圆的一般方程的相关知识可以得到问题的答案,需要掌握圆的一般方程的特点:(1)①x2和y2的系数相同,不等于0.②没有xy这样的二次项;(2)圆的一般方程中有三个特定的系数D、E、F,因之只要求出这三个系数,圆的方程就确定了;(3)、与圆的标准方程相比较,它是一种特殊的二元二次方程,代数特征明显,圆的标准方程则指出了圆心坐标与半径大小,几何特征较明显.
-
科目: 来源: 题型:
查看答案和解析>>【题目】给定两个命题,P:对任意实数x都有ax2+ax+1>0恒成立;Q:关于x的方程x2﹣x+a=0有实数根;如果P与Q中有且仅有一个为真命题,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知焦点在
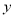 轴上的椭圆
轴上的椭圆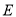 的中心是原点
的中心是原点 ,离心率为双曲线
,离心率为双曲线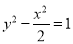 离心率的一半,直线
离心率的一半,直线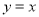 被椭圆
被椭圆 截得的线段长为
截得的线段长为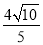 .直线
.直线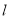 :
: 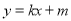 与
与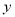 轴交于点
轴交于点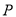 ,与椭圆
,与椭圆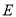 交于
交于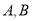 两个相异点,且
两个相异点,且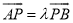 .
.(1)求椭圆
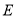 的方程;
的方程;(2)是否存在实数
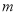 ,使
,使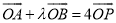 ?若存在,求
?若存在,求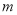 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2﹣mx+1﹣m2 , 若|f(x)|在[0,1]上单调递增,则实数m的取值范围 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2﹣lnx.
(1)求曲线f(x)在点(1,f(1))处的切线方程;
(2)求函数f(x)的单调递减区间:
(3)设函数g(x)=f(x)﹣x2+ax,a>0,若x∈(O,e]时,g(x)的最小值是3,求实数a的值.(e为自然对数的底数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
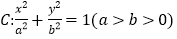 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线x﹣y+
,以原点为圆心,椭圆的短半轴长为半径的圆与直线x﹣y+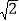 =0相切.
=0相切.(Ⅰ)求椭圆C的方程;
(Ⅱ)若过点M(2,0)的直线与椭圆C相交于两点A,B,当
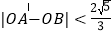 时,求直线斜率的取值范围.
时,求直线斜率的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设定义在区间
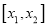 上的函数
上的函数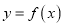 的图象为
的图象为 ,
, 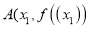 、
、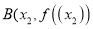 ,且
,且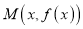 为图象
为图象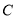 上的任意一点,
上的任意一点, 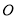 为坐标原点,当实数
为坐标原点,当实数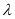 满足
满足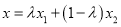 时,记向量
时,记向量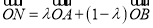 ,若
,若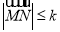 恒成立,则称函数
恒成立,则称函数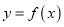 在区间
在区间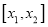 上可在标准
上可在标准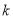 下线性近似,其中
下线性近似,其中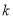 是一个确定的正数.
是一个确定的正数.(1)设函数
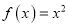 在区间
在区间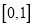 上可在标准
上可在标准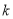 下线性近似,求
下线性近似,求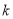 的取值范围;
的取值范围;(2)已知函数
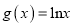 的反函数为
的反函数为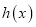 ,函数
,函数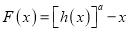 ,(
,( 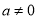 ),点
),点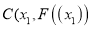 、
、 ,记直线
,记直线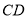 的斜率为
的斜率为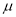 ,若
,若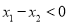 ,问:是否存在
,问:是否存在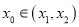 ,使
,使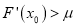 成立?若存在,求
成立?若存在,求 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
相关试题

