【题目】已知直线l的方程为ρsin(θ+ ![]() )=
)= ![]() ,圆C的方程为
,圆C的方程为 ![]() (θ为参数).
(θ为参数).
(1)把直线l和圆C的方程化为普通方程;
(2)求圆C上的点到直线l距离的最大值.
参考答案:
【答案】
(1)解:线l的方程为ρsin(θ+ ![]() )=
)= ![]() ,即
,即 ![]() sinθ+
sinθ+ ![]() cosθ=
cosθ= ![]() ,化为直角坐标方程为 x+y﹣2=0.
,化为直角坐标方程为 x+y﹣2=0.
把圆C的方程为 ![]() (θ为参数),利用同角三角函数的基本关系,消去θ,化为普通方程为 x2+y2=1
(θ为参数),利用同角三角函数的基本关系,消去θ,化为普通方程为 x2+y2=1
(2)解:圆心(0,0)到直线l的距离d= ![]() =
= ![]() ,半径为1,故圆C上的点到直线l距离的最大值为d+r=
,半径为1,故圆C上的点到直线l距离的最大值为d+r= ![]() +1
+1
【解析】(1)利用和角的正弦函数公式、以及x=ρcosθ、y=ρsinθ,即可求得该直线的直角坐标方程.(2)把圆C的方程利用同角三角函数的基本关系,消去θ,化为普通方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=lnx﹣mx(m∈R).
(1)若曲线y=f(x)过点P(1,﹣1),求曲线y=f(x)在点P的切线方程;
(2)若f(x)≤0恒成立求m的取值范围;
(3)求函数f(x)在区间[1,e]上最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a>0且满足不等式22a+1>25a﹣2.
(1)求实数a的取值范围;
(2)求不等式loga(3x+1)<loga(7﹣5x);
(3)若函数y=loga(2x﹣1)在区间[1,3]有最小值为﹣2,求实数a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市电视台为了宣传举办问答活动,随机对该市15~65岁的人群抽样了
 人,回答问题计结果如下图表所示:
人,回答问题计结果如下图表所示:
(1)分别求出
 的值;
的值;(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,则第2,3,4组每组各抽取多少人?
(3)在(2)的前提下,电视台决定在所抽取的6人中随机抽取2人颁发幸运奖,求所抽取的人中第2组至少有1人获得幸运奖的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
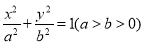 的右焦点与抛物线
的右焦点与抛物线 的焦点重合,且该椭圆的离心率与双曲线
的焦点重合,且该椭圆的离心率与双曲线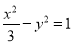 的离心率互为倒数.
的离心率互为倒数.(1)求椭圆的方程;
(2)设直线
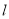 与椭圆相交于不同的两点
与椭圆相交于不同的两点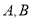 ,已知点
,已知点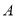 的坐标为
的坐标为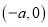 ,点
,点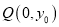 在线段
在线段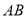 的垂直平分线上,且
的垂直平分线上,且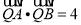 ,求
,求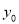 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2x
(1)试求函数F(x)=f(x)+f(2x),x∈(﹣∞,0]的最大值;
(2)若存在x∈(﹣∞,0),使|af(x)﹣f(2x)|>1成立,试求a的取值范围;
(3)当a>0,且x∈[0,15]时,不等式f(x+1)≤f[(2x+a)2]恒成立,求a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程x2+y2-2(t+3)x+2(1-4t2)y+16t4+9=0(t∈R)的图形是圆.
(1)求t的取值范围;
(2)求圆的面积取最大值时t的值;
(3)若点P(3,4t2)恒在所给圆内,求t的取值范围.
相关试题

