【题目】已知方程x2+y2-2(t+3)x+2(1-4t2)y+16t4+9=0(t∈R)的图形是圆.
(1)求t的取值范围;
(2)求圆的面积取最大值时t的值;
(3)若点P(3,4t2)恒在所给圆内,求t的取值范围.
参考答案:
【答案】(1)-![]() <t<1;(2)t=
<t<1;(2)t=![]() ;(3)0<t<
;(3)0<t<![]() .
.
【解析】
(1)先化圆的标准方程,再根据半径大于零得不等式,解得t的取值范围;(2)根据半径最大时面积最大,转化为求半径最大值,再根据二次函数性质求最大值取法即得结果;(3)根据条件列不等式,解得结果.
(1)方程即(x-t-3)2+(y+1-4t2)2=-7t2+6t+1,
∴r2=-7t2+6t+1>0,∴-![]() <t<1.
<t<1.
(2)∵r=![]() ,
,
∴当t=![]() ∈(-
∈(-![]() )时,rmax=
)时,rmax=![]() .
.
故当t=![]() 时,圆的面积最大.
时,圆的面积最大.
(3)当且仅当32+(4t2)2-2(t+3)×3+2(1-4t2)×4t2+16t4+9<0时,点P在圆内,
∴8t2-6t<0即0<t<![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l的方程为ρsin(θ+
 )=
)=  ,圆C的方程为
,圆C的方程为  (θ为参数).
(θ为参数).
(1)把直线l和圆C的方程化为普通方程;
(2)求圆C上的点到直线l距离的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
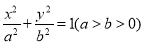 的右焦点与抛物线
的右焦点与抛物线 的焦点重合,且该椭圆的离心率与双曲线
的焦点重合,且该椭圆的离心率与双曲线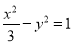 的离心率互为倒数.
的离心率互为倒数.(1)求椭圆的方程;
(2)设直线
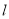 与椭圆相交于不同的两点
与椭圆相交于不同的两点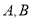 ,已知点
,已知点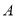 的坐标为
的坐标为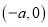 ,点
,点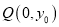 在线段
在线段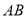 的垂直平分线上,且
的垂直平分线上,且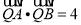 ,求
,求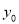 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2x
(1)试求函数F(x)=f(x)+f(2x),x∈(﹣∞,0]的最大值;
(2)若存在x∈(﹣∞,0),使|af(x)﹣f(2x)|>1成立,试求a的取值范围;
(3)当a>0,且x∈[0,15]时,不等式f(x+1)≤f[(2x+a)2]恒成立,求a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某圆圆心在x轴上,半径长为5,且截y轴所得线段长为8,求该圆的标准方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 .
.(1)当
 时,求
时,求 的定义域;
的定义域;(2)若函数的定义域为非空集合,求实数
 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,把函数
,把函数  的图象向右平移
的图象向右平移  个单位,得到函数
个单位,得到函数  的图象,若
的图象,若  是
是  在
在  内的两根,则
内的两根,则  的值为( )
的值为( )
A.
B.
C.
D.
相关试题

