【题目】已知数列![]() 满足
满足![]() ,
, ![]() ,其中
,其中![]() ,
, ![]() ,
, ![]() 为非零常数.
为非零常数.
(1)若![]() ,
, ![]() ,求证:
,求证: ![]() 为等比数列,并求数列
为等比数列,并求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 是公差不等于零的等差数列.
是公差不等于零的等差数列.
①求实数![]() ,
, ![]() 的值;
的值;
②数列![]() 的前
的前![]() 项和
项和![]() 构成数列
构成数列![]() ,从
,从![]() 中取不同的四项按从小到大排列组成四项子数列.试问:是否存在首项为
中取不同的四项按从小到大排列组成四项子数列.试问:是否存在首项为![]() 的四项子数列,使得该子数列中的所有项之和恰好为2017?若存在,求出所有满足条件的四项子数列;若不存在,请说明理由.
的四项子数列,使得该子数列中的所有项之和恰好为2017?若存在,求出所有满足条件的四项子数列;若不存在,请说明理由.
参考答案:
【答案】(1)![]() (2)①
(2)①![]() ,
, ![]() ,
, ![]() .②
.②![]() ,
, ![]() ,
, ![]()
【解析】试题分析:(1)利用等比数列定义证明,即寻找![]() 与
与![]() 比例关系:利用
比例关系:利用![]() 代入化简可得
代入化简可得![]() .最后说明各项非零.(2)①令
.最后说明各项非零.(2)①令![]() ,2,3,根据等差数列性质得
,2,3,根据等差数列性质得![]() ,列出关于
,列出关于![]() ,
, ![]() 的二元一次方程组,解得
的二元一次方程组,解得![]() ,
, ![]() 的值;再验证满足题意. ②先求数列
的值;再验证满足题意. ②先求数列![]() 的前
的前![]() 项和
项和![]() ,再讨论四项奇偶性:三个奇数一个偶数、或者一个奇数三个偶数.将奇偶性代入化简讨论,直至确定.
,再讨论四项奇偶性:三个奇数一个偶数、或者一个奇数三个偶数.将奇偶性代入化简讨论,直至确定.
试题解析:解:(1)当![]() ,
, ![]() 时,
时, ![]()
![]()
![]() ,
,
![]() .
.
又![]() ,不然
,不然![]() ,这与
,这与![]() 矛盾,
矛盾,
![]() 为2为首项,3为公比的等比数列,
为2为首项,3为公比的等比数列,
![]() ,
, ![]() .
.
(2)①设![]()
![]() ,
,
由![]() 得
得![]()
![]() ,
,
![]()
![]()
![]() ,
,
![]()
![]()
![]()
![]()
对任意![]() 恒成立.
恒成立.
令![]() ,2,3,解得,
,2,3,解得, ![]() ,
, ![]() ,
, ![]() .
.
经检验,满足题意.
综上, ![]() ,
, ![]() ,
, ![]() .
.
②由①知![]() .
.
设存在这样满足条件的四元子列,观察到2017为奇数,这四项或者三个奇数一个偶数、或者一个奇数三个偶数.
1°若三个奇数一个偶数,设![]() ,
, ![]() ,
, ![]() ,
, ![]() 是满足条件的四项,
是满足条件的四项,
则![]()
![]() ,
,
![]()
![]() ,这与1007为奇数矛盾,不合题意舍去.
,这与1007为奇数矛盾,不合题意舍去.
2°若一个奇数三个偶数,设![]() ,
, ![]() ,
, ![]() ,
, ![]() 是满足条件的四项,
是满足条件的四项,
则![]()
![]() ,
, ![]() .
.
由504为偶数知, ![]() ,
, ![]() ,
, ![]() 中一个偶数两个奇数或者三个偶数.
中一个偶数两个奇数或者三个偶数.
1)若![]() ,
, ![]() ,
, ![]() 中一个偶数两个奇数,不妨设
中一个偶数两个奇数,不妨设![]() ,
, ![]() ,
, ![]() ,
,
则![]()
![]() ,这与251为奇数矛盾.
,这与251为奇数矛盾.
2)若![]() ,
, ![]() ,
, ![]() 均为偶数,不妨设
均为偶数,不妨设![]() ,
, ![]() ,
, ![]() ,
,
则![]() ,继续奇偶分析知
,继续奇偶分析知![]() ,
, ![]() ,
, ![]() 中两奇数一个偶数,
中两奇数一个偶数,
不妨设![]() ,
, ![]() ,
, ![]() ,则
,则![]()
![]() .
.
因为![]() ,
, ![]() 均为偶数,所以
均为偶数,所以![]() 为奇数,不妨设
为奇数,不妨设![]() ,
,
当![]() 时,
时, ![]()
![]() ,
, ![]() ,检验得
,检验得![]() ,
, ![]() ,
, ![]() ,
,
当![]() 时,
时, ![]()
![]() ,
, ![]() ,检验得
,检验得![]() ,
, ![]() ,
, ![]() ,
,
当![]() 时,
时, ![]()
![]() ,
, ![]() ,检验得
,检验得![]() ,
, ![]() ,
, ![]() ,
,
即![]() ,
, ![]() ,
, ![]() ,
, ![]() 或者
或者![]() ,
, ![]() ,
, ![]() ,
, ![]() 或者
或者![]() ,
, ![]() ,
, ![]() ,
, ![]() 满足条件,
满足条件,
综上所述, ![]() ,
, ![]() ,
, ![]() 为全部满足条件的四元子列.
为全部满足条件的四元子列.
-
科目: 来源: 题型:
查看答案和解析>>【题目】执行下面的程序框图,如果输入的t=0.01,则输出的n=( )

A.5
B.6
C.7
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=
 sin
sin  ,若存在f(x)的极值点x0满足x02+[f(x0)]2<m2 , 则m的取值范围是( )
,若存在f(x)的极值点x0满足x02+[f(x0)]2<m2 , 则m的取值范围是( )
A.(﹣∞,﹣6)∪(6,+∞)
B.(﹣∞,﹣4)∪(4,+∞)
C.(﹣∞,﹣2)∪(2,+∞)
D.(﹣∞,﹣1)∪(1,+∞) -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分10分)已知等差数列{an}满足a1+a2=10,a4-a3=2.
(1)求{an}的通项公式.
(2)设等比数列{bn}满足b2=a3,b3=a7.问:b6与数列{an}的第几项相等?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列{an}满足a3=2,前3项和为S3=
 .
.(1)求{an}的通项公式;
(2)设等比数列{bn}满足b1=a1,b4=a15,求{bn}的前n项和Tn.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知两定点
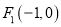 ,
, 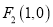 和一动点
和一动点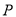 ,给出下列结论:
,给出下列结论:①若
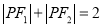 ,则点
,则点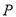 的轨迹是椭圆;
的轨迹是椭圆;②若
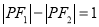 ,则点
,则点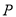 的轨迹是双曲线;
的轨迹是双曲线;③若
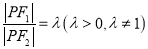 ,则点
,则点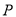 的轨迹是圆;
的轨迹是圆;④若
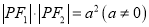 ,则点
,则点 的轨迹关于原点对称;
的轨迹关于原点对称;⑤若直线
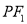 与
与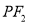 斜率之积等于
斜率之积等于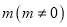 ,则点
,则点 的轨迹是椭圆(除长轴两端点).
的轨迹是椭圆(除长轴两端点).其中正确的是__________(填序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 :
:  (
(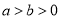 )的左焦点为
)的左焦点为 ,左准线方程为
,左准线方程为 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)已知直线
 交椭圆
交椭圆 于
于 ,
,  两点.
两点.①若直线
 经过椭圆
经过椭圆 的左焦点
的左焦点 ,交
,交 轴于点
轴于点 ,且满足
,且满足 ,
,  .求证:
.求证:  为定值;
为定值;②若
 (
( 为原点),求
为原点),求 面积的取值范围.
面积的取值范围.
相关试题

