【题目】已知等差数列{an}满足a3=2,前3项和为S3=![]() .
.
(1)求{an}的通项公式;
(2)设等比数列{bn}满足b1=a1,b4=a15,求{bn}的前n项和Tn.
参考答案:
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)根据等差数列的基本量运算解出![]() 和
和![]() ,代入公式算出等差数列
,代入公式算出等差数列![]() 的通项公式;(2)计算出等比数列的首项和公比,代入求和公式计算.
的通项公式;(2)计算出等比数列的首项和公比,代入求和公式计算.
试题解析:
(1)设{an}的公差为d,由已知得

解得a1=1,d=![]() ,
,
故{an}的通项公式an=1+![]() ,即an=
,即an=![]() .
.
(2)由(1)得b1=1,b4=a15=![]() =8.
=8.
设{bn}的公比为q,则q3=![]() =8,从而q=2,
=8,从而q=2,
故{bn}的前n项和Tn=![]() =2n-1.
=2n-1.
点睛:本题考查等差数列的基本量运算求通项公式以及等比数列的前n项和,属于基础题. 在数列求和中,最常见最基本的求和就是等差数列、等比数列中的求和,这时除了熟练掌握求和公式外还要熟记一些常见的求和结论,再就是分清数列的项数,比如题中给出的![]() ,以免在套用公式时出错.
,以免在套用公式时出错.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=
 sin
sin  ,若存在f(x)的极值点x0满足x02+[f(x0)]2<m2 , 则m的取值范围是( )
,若存在f(x)的极值点x0满足x02+[f(x0)]2<m2 , 则m的取值范围是( )
A.(﹣∞,﹣6)∪(6,+∞)
B.(﹣∞,﹣4)∪(4,+∞)
C.(﹣∞,﹣2)∪(2,+∞)
D.(﹣∞,﹣1)∪(1,+∞) -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分10分)已知等差数列{an}满足a1+a2=10,a4-a3=2.
(1)求{an}的通项公式.
(2)设等比数列{bn}满足b2=a3,b3=a7.问:b6与数列{an}的第几项相等?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
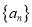 满足
满足 ,
, 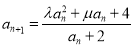 ,其中
,其中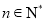 ,
, 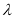 ,
, 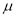 为非零常数.
为非零常数.(1)若
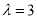 ,
, 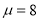 ,求证:
,求证: 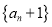 为等比数列,并求数列
为等比数列,并求数列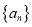 的通项公式;
的通项公式;(2)若数列
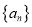 是公差不等于零的等差数列.
是公差不等于零的等差数列.①求实数
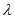 ,
, 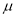 的值;
的值;②数列
 的前
的前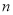 项和
项和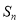 构成数列
构成数列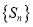 ,从
,从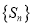 中取不同的四项按从小到大排列组成四项子数列.试问:是否存在首项为
中取不同的四项按从小到大排列组成四项子数列.试问:是否存在首项为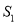 的四项子数列,使得该子数列中的所有项之和恰好为2017?若存在,求出所有满足条件的四项子数列;若不存在,请说明理由.
的四项子数列,使得该子数列中的所有项之和恰好为2017?若存在,求出所有满足条件的四项子数列;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知两定点
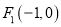 ,
, 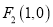 和一动点
和一动点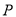 ,给出下列结论:
,给出下列结论:①若
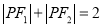 ,则点
,则点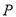 的轨迹是椭圆;
的轨迹是椭圆;②若
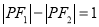 ,则点
,则点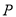 的轨迹是双曲线;
的轨迹是双曲线;③若
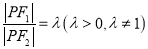 ,则点
,则点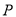 的轨迹是圆;
的轨迹是圆;④若
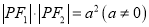 ,则点
,则点 的轨迹关于原点对称;
的轨迹关于原点对称;⑤若直线
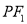 与
与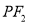 斜率之积等于
斜率之积等于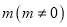 ,则点
,则点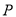 的轨迹是椭圆(除长轴两端点).
的轨迹是椭圆(除长轴两端点).其中正确的是__________(填序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 :
:  (
(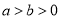 )的左焦点为
)的左焦点为 ,左准线方程为
,左准线方程为 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)已知直线
 交椭圆
交椭圆 于
于 ,
,  两点.
两点.①若直线
 经过椭圆
经过椭圆 的左焦点
的左焦点 ,交
,交 轴于点
轴于点 ,且满足
,且满足 ,
,  .求证:
.求证:  为定值;
为定值;②若
 (
(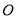 为原点),求
为原点),求 面积的取值范围.
面积的取值范围.
-
科目: 来源: 题型:
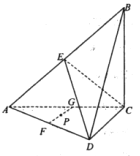
查看答案和解析>>【题目】如图,在四面体
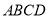 中,平面
中,平面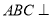 平面
平面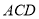 ,
, 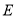 ,
, 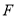 ,
, 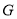 分别为
分别为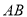 ,
, 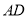 ,
, 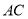 的中点,
的中点, 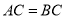 ,
, 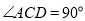 .
.(1)求证:
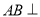 平面
平面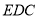 ;
;(2)若
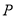 为
为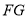 上任一点,证明
上任一点,证明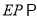 平面
平面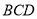 .
.
相关试题

