【题目】如图,直三棱柱![]() 的底面为正三角形,
的底面为正三角形,![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 的中点.
的中点.

⑴若![]() ,求证:
,求证:![]() 平面
平面![]() ;
;
⑵若![]() 为
为![]() 中点,
中点,![]() ,四棱锥
,四棱锥![]() 的体积为
的体积为![]() ,求三棱锥
,求三棱锥![]() 的表面积.
的表面积.
参考答案:
【答案】⑴证明见解析;⑵![]() .
.
【解析】
试题分析:⑴由三棱柱![]() 是直三棱柱
是直三棱柱![]()
![]() ,又
,又![]() ,
, ![]()
![]()
![]() 平面
平面![]()
![]()
![]() ,又四边形
,又四边形![]() 为正方形
为正方形![]()
![]() ,又
,又![]()
![]()
![]()
![]() 以
以![]() 平面
平面![]() ;⑵由
;⑵由![]() 是正三角形
是正三角形![]()
![]() ,又
,又![]()
![]()
![]() 平面
平面![]()
![]()
![]() .设
.设![]() ,由
,由![]()
![]()
![]() .又
.又![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
试题解析: ⑴证明:如图,因为三棱柱![]() 是直三棱柱,所以
是直三棱柱,所以![]() ,
,
又![]() 是正三角形
是正三角形![]() 的边
的边![]() 的中点,所以
的中点,所以![]() ,又
,又![]() ,
,
所以![]() 平面
平面![]() ,则
,则![]() ,……………………3分
,……………………3分
连接![]() ,易知四边形
,易知四边形![]() 为正方形,则
为正方形,则![]() ,
,
又![]() ,则
,则![]() ,因为
,因为![]() ,所以
,所以![]() 平面
平面![]() .……6分
.……6分
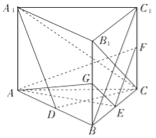
⑵解:因为![]() 是正三角形,所以
是正三角形,所以![]() ,
,
又三棱柱![]() 是直三棱柱,所以
是直三棱柱,所以![]() ,
,
所以![]() 平面
平面![]() ,所以
,所以![]() .………………………………7分
.………………………………7分
设![]() ,由题可知,
,由题可知,![]() ,所以
,所以![]() .………………8分
.………………8分
在![]() 中,
中,![]() ,
,
所以![]() ,∴
,∴![]() .……10分
.……10分
故三棱锥![]() 的表面积
的表面积![]() .……12分
.……12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等比数列
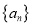 中,已知
中,已知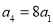 ,且
,且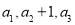 成等差数列.
成等差数列.(1)求数列
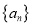 的通项公式;
的通项公式;(2)求数列
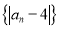 的前
的前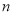 项和
项和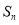 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:极坐标与参数方程
已知平面直角坐标系
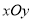 ,以
,以 为极点,
为极点, 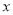 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线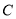 的参数方程为
的参数方程为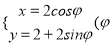 为参数). 点
为参数). 点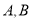 是曲线
是曲线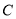 上两点,点
上两点,点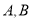 的极坐标分别为
的极坐标分别为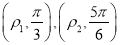 .
.(1)写出曲线
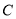 的普通方程和极坐标方程;
的普通方程和极坐标方程;(2)求
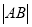 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的程序框图表示的算法功能是( )
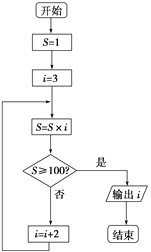
A. 计算小于100的奇数的连乘积
B. 计算从1开始的连续奇数的连乘积
C. 从1开始的连续奇数的连乘积,当乘积大于或等于100时,计算奇数的个数
D. 计算1×3×5×…×n≥100时的最小的n的值
-
科目: 来源: 题型:
查看答案和解析>>【题目】
已知函数
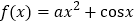 (
(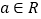 ),记
),记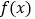 的导函数为
的导函数为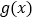 .
.(1)证明:当
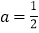 时,
时,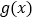 在
在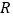 上单调递增;
上单调递增;(2)若
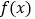 在
在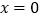 处取得极小值,求
处取得极小值,求 的取值范围;
的取值范围; (3)设函数
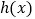 的定义域为
的定义域为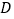 ,区间
,区间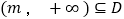 ,若
,若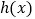 在
在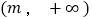 上是单调函数,
上是单调函数,则称
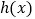 在
在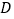 上广义单调.试证明函数
上广义单调.试证明函数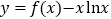 在
在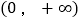 上广义单调.
上广义单调. -
科目: 来源: 题型:
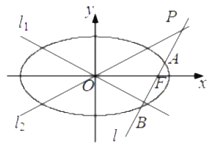
查看答案和解析>>【题目】已知椭圆
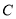 方程为
方程为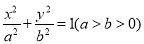 ,双曲线
,双曲线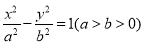 的两条渐近线分别为
的两条渐近线分别为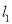 ,
,  ,过椭圆
,过椭圆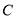 的右焦点作直线
的右焦点作直线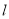 ,使
,使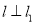 ,又
,又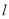 与
与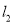 交于点
交于点 ,设直线
,设直线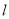 与椭圆
与椭圆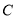 的两个交点由上至下依次为
的两个交点由上至下依次为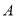 ,
, 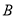 .
. 
(1)若
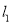 与
与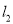 所成的锐角为
所成的锐角为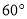 ,且双曲线的焦距为4,求椭圆
,且双曲线的焦距为4,求椭圆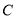 的方程;
的方程;(2)求
 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,底面
中,底面 是矩形,平面
是矩形,平面 平面
平面 分别为棱
分别为棱 的中点.求证:
的中点.求证:
(1)
 平面
平面 ;
;(2)
 平面
平面 .
.
相关试题

