【题目】选修4-4:极坐标与参数方程
已知平面直角坐标系![]() ,以
,以![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的参数方程为
的参数方程为![]() 为参数). 点
为参数). 点![]() 是曲线
是曲线![]() 上两点,点
上两点,点![]() 的极坐标分别为
的极坐标分别为![]() .
.
(1)写出曲线![]() 的普通方程和极坐标方程;
的普通方程和极坐标方程;
(2)求![]() 的值.
的值.
参考答案:
【答案】(1)![]() ;(2)4.
;(2)4.
【解析】试题分析:(1)曲线![]() 的参数方程为
的参数方程为![]() ,
, ![]() 为参数),消去参数
为参数),消去参数![]() ,化为普通方程是
,化为普通方程是![]() ,由
,由![]() ,
, ![]() 为参数),曲线
为参数),曲线![]() 的普通方程
的普通方程![]() 可化为极坐标
可化为极坐标![]() ,
, ![]() 为参数);(2)方法1:由
为参数);(2)方法1:由![]() 是圆
是圆![]() 上的两点,且知
上的两点,且知![]() ,
, ![]() 为直径,从而求得
为直径,从而求得![]() .方法2:由两点
.方法2:由两点![]() 化为直角坐标中点的坐标,利用两点间距离公式求得
化为直角坐标中点的坐标,利用两点间距离公式求得![]() 、
、![]() 两点间的距离.
两点间的距离.
试题解析:(1)![]() 曲线
曲线![]() 的参数方程为
的参数方程为![]() ,
, ![]() 为参数),
为参数),
消去参数![]() ,化为普通方程是
,化为普通方程是![]() ;
;
由![]() ,
, ![]() 为参数).
为参数).
![]() 曲线
曲线![]() 的普通方程
的普通方程![]() 可化为极坐标
可化为极坐标![]() ,
, ![]() 为参数).
为参数).
(2)方法1:由![]() 是圆
是圆![]() 上的两点,
上的两点,
且知![]() ,
, ![]() 为直径,
为直径, ![]() .
.
方法2:由两点![]() 化为直角坐标中点的坐标是
化为直角坐标中点的坐标是![]() ,
, ![]() ,
,
![]() 、
、![]() 两点间的距离为
两点间的距离为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆
 :
:  的离心率与双曲线
的离心率与双曲线 的离心率互为倒数,且椭圆的长轴长为4.
的离心率互为倒数,且椭圆的长轴长为4.(1)求椭圆
 的标准方程;
的标准方程;(2)若直线
 交椭圆
交椭圆 于
于 ,
,  两点,
两点,  (
( )为椭圆
)为椭圆 上一点,求
上一点,求 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校高三文科500名学生参加了5月份的模拟考试,学校为了了解高三文科学生的数学、语文情况,利用随机数表法从中抽取100名学生的成绩进行统计分析,抽出的100名学生的数学、语文成绩如下表:

(1)将学生编号为:001,002,003,……,499,500.若从第5行第5列的数开始右读,请你依次写出最先抽出的5个人的编号(下面是摘自随机数表的第4行至第7行)

(2)若数学的优秀率为
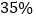 ,求
,求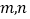 的值;
的值;(3)在语文成绩为良好的学生中,已知
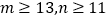 ,求数学成绩“优”比“良”的人数少的概率.
,求数学成绩“优”比“良”的人数少的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】在等比数列
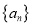 中,已知
中,已知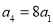 ,且
,且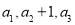 成等差数列.
成等差数列.(1)求数列
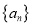 的通项公式;
的通项公式;(2)求数列
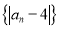 的前
的前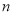 项和
项和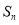 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的程序框图表示的算法功能是( )
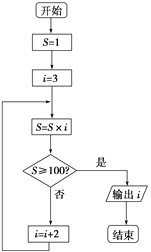
A. 计算小于100的奇数的连乘积
B. 计算从1开始的连续奇数的连乘积
C. 从1开始的连续奇数的连乘积,当乘积大于或等于100时,计算奇数的个数
D. 计算1×3×5×…×n≥100时的最小的n的值
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直三棱柱
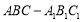 的底面为正三角形,
的底面为正三角形,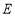 、
、 、
、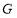 分别是
分别是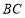 、
、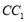 、
、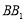 的中点.
的中点.
⑴若
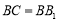 ,求证:
,求证: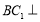 平面
平面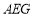 ;
;⑵若
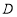 为
为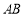 中点,
中点,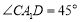 ,四棱锥
,四棱锥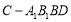 的体积为
的体积为 ,求三棱锥
,求三棱锥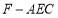 的表面积.
的表面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】
已知函数
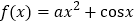 (
(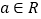 ),记
),记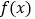 的导函数为
的导函数为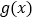 .
.(1)证明:当
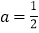 时,
时,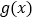 在
在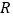 上单调递增;
上单调递增;(2)若
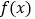 在
在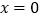 处取得极小值,求
处取得极小值,求 的取值范围;
的取值范围; (3)设函数
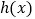 的定义域为
的定义域为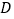 ,区间
,区间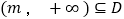 ,若
,若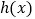 在
在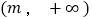 上是单调函数,
上是单调函数,则称
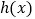 在
在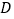 上广义单调.试证明函数
上广义单调.试证明函数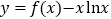 在
在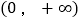 上广义单调.
上广义单调.
相关试题

