【题目】已知函数![]() 和
和![]() 在
在![]() 的图象如图所示:
的图象如图所示:
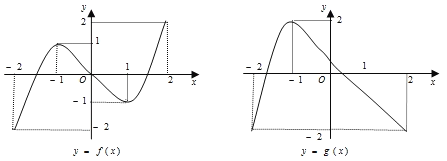
给出下列四个命题:
(1)方程![]() 有且仅有6个根;
有且仅有6个根;
(2)方程![]() 有且仅有3个根;
有且仅有3个根;
(3)方程![]() 有且仅有5个根;
有且仅有5个根;
(4)方程![]() 有且仅有4个根.
有且仅有4个根.
其中正确命题的个数是( )
A. 4个B. 3个C. 2个D. 1个
参考答案:
【答案】B
【解析】
把复合函数的定义域和值域进行对接,看满足外层函数为零时内层函数有几个自变量与之相对应.通过![]() 可知函数
可知函数![]() 有3个解,
有3个解,![]() 有2个解,然后具体分析①②③④,进而可得出正确的结论.
有2个解,然后具体分析①②③④,进而可得出正确的结论.
由图象可得![]() .
.
对于(1),由于满足方程![]() 的
的![]() 有三个不同值,一个值在2与1之间,一个值为0,一个值在1到2之间,由
有三个不同值,一个值在2与1之间,一个值为0,一个值在1到2之间,由![]() 的图象可得每个值
的图象可得每个值![]() 对应了2个
对应了2个![]() 值,故满足
值,故满足![]() 的
的![]() 值有6个,即方程
值有6个,即方程![]() 有且仅有6个根,故(1)正确.
有且仅有6个根,故(1)正确.
对于(2),由图可得满足![]() 的
的![]() 有两个,一个值处于2与1之间,由
有两个,一个值处于2与1之间,由![]() 的图象可得此时对应一个
的图象可得此时对应一个![]() 值;另一个值处于0与1之间,由
值;另一个值处于0与1之间,由![]() 的图象可得此时对应三个
的图象可得此时对应三个![]() 值,因此该方程有且仅有4个根.故(2)不正确.
值,因此该方程有且仅有4个根.故(2)不正确.
对于(3),由于满足方程![]() 的
的![]() 有3个不同的值,从图中可知一个
有3个不同的值,从图中可知一个![]() 等于0,一个
等于0,一个![]() ,一个
,一个![]() .而当
.而当![]() 对应了3个不同的
对应了3个不同的![]() 值;当
值;当![]() 时,只对应一个
时,只对应一个![]() 值;当
值;当![]() 时,也只对应一个
时,也只对应一个![]() 值.故满足方程
值.故满足方程![]() 的
的![]() 值共有5个,故(3)正确.
值共有5个,故(3)正确.
对于(4),由于满足方程![]() 的
的![]() 值有2个,而结合图象可得每个
值有2个,而结合图象可得每个![]() 值对应2个不同的
值对应2个不同的![]() 值,故满足方程
值,故满足方程![]() 的
的![]() 值有4个,即方程
值有4个,即方程![]() 有且仅有4个根,故(4)正确.
有且仅有4个根,故(4)正确.
综上得(1)(3)(4)正确.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
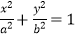 (a>b>0)的左焦点为F1(﹣
(a>b>0)的左焦点为F1(﹣ 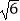 ,0),e=
,0),e= 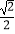 . (Ⅰ)求椭圆C的方程;
. (Ⅰ)求椭圆C的方程;
(Ⅱ)如图,设R(x0 , y0)是椭圆C上一动点,由原点O向圆(x﹣x0)2+(y﹣y0)2=4引两条切线,分别交椭圆于点P,Q,若直线OP,OQ的斜率存在,并记为k1 , k2 , 求证:k1k2为定值;
(Ⅲ)在(Ⅱ)的条件下,试问OP2+OQ2是否为定值?若是,求出该值;若不是,说明理由.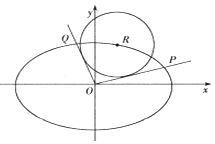
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出以下结论,其中正确结论的个数为( )
①函数
 的零点为
的零点为 ,则函数
,则函数 的图象经过点
的图象经过点 时,函数值一定变号.
时,函数值一定变号.②相邻两个零点之间的所有函数值保持同号.
③函数
 在区间
在区间 上连续,若满足
上连续,若满足 ,则方程
,则方程 在区间
在区间 上一定有实根.
上一定有实根.④“二分法”对连续不断的函数的所有零点都有效.
A. 0个B. 1个C. 2个D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
 是平面直角坐标系中两两不同的四点,若
是平面直角坐标系中两两不同的四点,若 ,
, ,且
,且 ,则称
,则称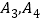 调和分割
调和分割 .已知平面上的点
.已知平面上的点 调和分割点
调和分割点 ,则下列说法正确的是
,则下列说法正确的是A.
 可能线段
可能线段 的中点
的中点B.
 可能线段
可能线段 的中点
的中点C.
 可能同时在线段
可能同时在线段 上
上D.
 不可能同时在线段
不可能同时在线段 的延长线上
的延长线上 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ex﹣1﹣x﹣ax2 . (Ⅰ)当a=0时,求证:f(x)≥0;
(Ⅱ)当x≥0时,若不等式f(x)≥0恒成立,求实数a的取值范围;
(Ⅲ)若x>0,证明(ex﹣1)ln(x+1)>x2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】以直角坐标系xOy中,直线l:y=x,圆C:
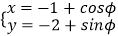 (φ为参数),以坐标原点为为极点,x轴的正半轴为极轴建立极坐标系. (Ⅰ)求直线l与圆C的极坐标方程;
(φ为参数),以坐标原点为为极点,x轴的正半轴为极轴建立极坐标系. (Ⅰ)求直线l与圆C的极坐标方程;
(Ⅱ)设直线l与圆C的交点为M,N,求△CMN的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|x﹣a|﹣
 x,(a>0). (Ⅰ)若a=3,解关于x的不等式f(x)<0;
x,(a>0). (Ⅰ)若a=3,解关于x的不等式f(x)<0;
(Ⅱ)若对于任意的实数x,不等式f(x)﹣f(x+a)<a2+ 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
相关试题

