【题目】设![]() 是平面直角坐标系中两两不同的四点,若
是平面直角坐标系中两两不同的四点,若![]() ,
,![]() ,且
,且![]() ,则称
,则称![]() 调和分割
调和分割![]() .已知平面上的点
.已知平面上的点![]() 调和分割点
调和分割点![]() ,则下列说法正确的是
,则下列说法正确的是
A. ![]() 可能线段
可能线段![]() 的中点
的中点
B. ![]() 可能线段
可能线段![]() 的中点
的中点
C. ![]() 可能同时在线段
可能同时在线段![]() 上
上
D. ![]() 不可能同时在线段
不可能同时在线段![]() 的延长线上
的延长线上
参考答案:
【答案】D
【解析】
由已知不妨设A(0,0)、B(1,0)、C(c,0)、D(d,0),
则(c,0)=λ(1,0),(d,0)=μ(1,0),
∴λ=c,μ=d;
代入![]() = 2得
= 2得![]() = 2;()
= 2;()
若C是线段AB的中点,则c=![]() ,代入()得,d不存在,
,代入()得,d不存在,
∴C不可能是线段AB的中点,A错误;同理B错误;
若C,D同时在线段AB上,则0c1,0d1,代入()得,c=d=1,
此时C和D点重合,与已知矛盾,∴C错误.
若C,D同时在线段AB的延长线上时,则λ>1.μ>1,
![]() ,这与
,这与![]() 矛盾,
矛盾,
所以C、D不可能同时在线段AB的延长线上.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解学生喜欢校内、校外开展活动的情况,某中学一课外活动小组在学校高一年级进行了问卷调查,问卷共100道题,每题1分,总分100分,该课外活动小组随机抽取了200名学生的问卷成绩(单位:分)进行统计,将数据按
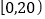 ,
,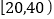 ,
,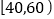 ,
,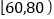 ,
,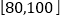 分成五组,绘制的频率分布直方图如图所示,若将不低于60分的称为
分成五组,绘制的频率分布直方图如图所示,若将不低于60分的称为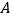 类学生,低于60分的称为
类学生,低于60分的称为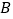 类学生.
类学生.
(1)根据已知条件完成下面
 列联表,能否在犯错误的概率不超过
列联表,能否在犯错误的概率不超过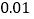 的前提下认为性别与是否为
的前提下认为性别与是否为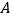 类学生有关系?
类学生有关系?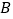 类
类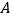 类
类合计
男
110
女
50
合计
(2)将频率视为概率,现在从该校高一学生中用随机抽样的方法每次抽取1人,共抽取3次,记被抽取的3人中
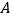 类学生的人数为
类学生的人数为 ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求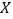 的分布列、期望
的分布列、期望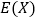 和方差
和方差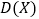 .
.参考公式:
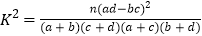 ,其中
,其中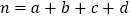 .
.参考临界值:
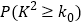
0.10
0.05
0.025
0.010
0.005
0.001
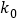
2.706
3.841
5.024
6.635
7.879
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
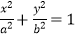 (a>b>0)的左焦点为F1(﹣
(a>b>0)的左焦点为F1(﹣ 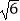 ,0),e=
,0),e= 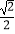 . (Ⅰ)求椭圆C的方程;
. (Ⅰ)求椭圆C的方程;
(Ⅱ)如图,设R(x0 , y0)是椭圆C上一动点,由原点O向圆(x﹣x0)2+(y﹣y0)2=4引两条切线,分别交椭圆于点P,Q,若直线OP,OQ的斜率存在,并记为k1 , k2 , 求证:k1k2为定值;
(Ⅲ)在(Ⅱ)的条件下,试问OP2+OQ2是否为定值?若是,求出该值;若不是,说明理由.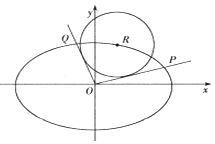
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出以下结论,其中正确结论的个数为( )
①函数
 的零点为
的零点为 ,则函数
,则函数 的图象经过点
的图象经过点 时,函数值一定变号.
时,函数值一定变号.②相邻两个零点之间的所有函数值保持同号.
③函数
 在区间
在区间 上连续,若满足
上连续,若满足 ,则方程
,则方程 在区间
在区间 上一定有实根.
上一定有实根.④“二分法”对连续不断的函数的所有零点都有效.
A. 0个B. 1个C. 2个D. 3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
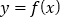 和
和 在
在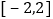 的图象如图所示:
的图象如图所示: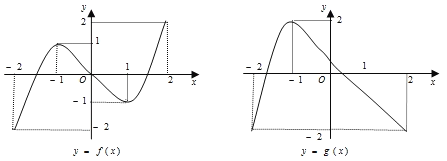
给出下列四个命题:
(1)方程
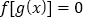 有且仅有6个根;
有且仅有6个根;(2)方程
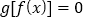 有且仅有3个根;
有且仅有3个根;(3)方程
 有且仅有5个根;
有且仅有5个根;(4)方程
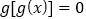 有且仅有4个根.
有且仅有4个根.其中正确命题的个数是( )
A. 4个B. 3个C. 2个D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ex﹣1﹣x﹣ax2 . (Ⅰ)当a=0时,求证:f(x)≥0;
(Ⅱ)当x≥0时,若不等式f(x)≥0恒成立,求实数a的取值范围;
(Ⅲ)若x>0,证明(ex﹣1)ln(x+1)>x2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】以直角坐标系xOy中,直线l:y=x,圆C:
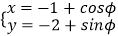 (φ为参数),以坐标原点为为极点,x轴的正半轴为极轴建立极坐标系. (Ⅰ)求直线l与圆C的极坐标方程;
(φ为参数),以坐标原点为为极点,x轴的正半轴为极轴建立极坐标系. (Ⅰ)求直线l与圆C的极坐标方程;
(Ⅱ)设直线l与圆C的交点为M,N,求△CMN的面积.
相关试题

