【题目】已知a是实数,函数f(x)=![]() (x-a).
(x-a).
(1)求函数f(x)的单调区间;
(2)设g(a)为f(x)在区间[0,2]上的最小值.
①写出g(a)的表达式;
②求a的取值范围,使得-6≤g(a)≤-2.
参考答案:
【答案】见解析
【解析】解 (1)函数的定义域为[0,+∞),
f′(x)=![]() +
+![]() =
=![]() (x>0).
(x>0).
若a≤0,则f′(x)>0,f(x)有单调递增区间[0,+∞).
若a>0,令f′(x)=0,得x=![]() ,
,
当0<x<![]() 时,f′(x)<0,
时,f′(x)<0,
当x>![]() 时,f′(x)>0.
时,f′(x)>0.
f(x)有单调递减区间[0,![]() ],有单调递增区间(
],有单调递增区间(![]() ,+∞).
,+∞).
(2)①由(1)知,若a≤0,f(x)在[0,2]上单调递增,
所以g(a)=f(0)=0.
若0<a<6,f(x)在[0,![]() ]上单调递减,在(
]上单调递减,在(![]() ,2]上单调递增,
,2]上单调递增,
所以g(a)=f(![]() )=-
)=-![]()
![]() .
.
若a≥6,f(x)在[0,2]上单调递减,所以g(a)=f(2)=![]() (2-a).
(2-a).
综上所述,g(a)=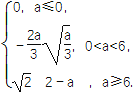
②令-6≤g(a)≤-2.若a≤0,无解.
若0<a<6,解得3≤a<6.
若a≥6,解得6≤a≤2+3![]() .
.
故a的取值范围为3≤a≤2+3![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列{an}中公差d≠0,有a1+a4=14,且a1,a2,a7成等比数列.
(Ⅰ)求{an}的通项公式an与前n项和公式Sn;
(Ⅱ)令bn=
 (k<0),若{bn}是等差数列,求数列{
(k<0),若{bn}是等差数列,求数列{ }的前n项和Tn.
}的前n项和Tn. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,BC边上的中线AD长为3,且BD=2,sinB=
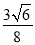 .
.(Ⅰ)求sin∠BAD的值;
(Ⅱ)求AC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设关于θ的方程
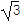 cosθ+sinθ+a=0在区间(0,2π)内有相异的两个实根α、β.
cosθ+sinθ+a=0在区间(0,2π)内有相异的两个实根α、β.(1)求实数a的取值范围;
(2)求α+β的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4,且位于x轴上方的点,A到抛物线准线的距离等于5,过A作AB垂直于y轴,垂足为B,OB的中点为M.
(1)求抛物线的方程;
(2)以M为圆心,MB为半径作圆M,当K(m,0)是x轴上一动点时,讨论直线AK与圆M的位置关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4,且位于x轴上方的点,A到抛物线准线的距离等于5,过A作AB垂直于y轴,垂足为B,OB的中点为M.
(1)求抛物线的方程;
(2)以M为圆心,MB为半径作圆M,当K(m,0)是x轴上一动点时,讨论直线AK与圆M的位置关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
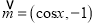 ,
,  ,设函数
,设函数 .
.(1)求函数
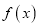 的最小正周期;
的最小正周期;(2)已知
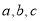 分别为三角形
分别为三角形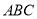 的内角对应的三边长,
的内角对应的三边长, 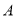 为锐角,
为锐角, 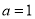 ,
,  ,且
,且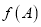 恰是函数
恰是函数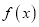 在
在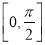 上的最大值,求
上的最大值,求 和三角形
和三角形 的面积.
的面积.
相关试题

