【题目】已知等差数列{an}中公差d≠0,有a1+a4=14,且a1,a2,a7成等比数列.
(Ⅰ)求{an}的通项公式an与前n项和公式Sn;
(Ⅱ)令bn=![]() (k<0),若{bn}是等差数列,求数列{
(k<0),若{bn}是等差数列,求数列{![]() }的前n项和Tn.
}的前n项和Tn.
参考答案:
【答案】(Ⅰ)an=4n-3,Sn==2n2-n; (Ⅱ)![]() .
.
【解析】试题分析:(1)利用等比数列的首项和公差建立方程求解即可;
(2)求出通项,利用裂项相消求和即可.
试题解析:
(Ⅰ)∵a1+a4=14,∴2a1+3d=14,①
∵a1,a2,a7成等比数列,∴![]() ,
,
即![]() ,②
,②
由①②得d2=4a1d,
∵d≠0,∴d=4a1,代入①解得d=4、a1=1,
∴an=a1+(n-1)d=4n-3,
Sn=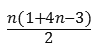 =2n2-n;
=2n2-n;
(Ⅱ)由(1)知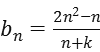 ,
,
∵{bn}是为等差数列,∴2b2=b1+b3,即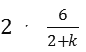 =
=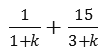 ,
,
解得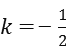 ,或k=0,
,或k=0,
由条件知, ,即bn=2n,
,即bn=2n,
则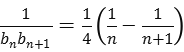
∴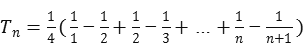
=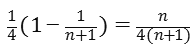
所以,Tn=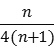 …
…
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列{an}的前3项和为6,前8项和为-4.
(1)求数列{an}的通项公式;
(2)设bn=(4-an)qn-1 (q≠0,n∈N*),求数列{bn}的前n项和Sn.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
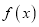 是定义在
是定义在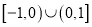 上的偶函数,当
上的偶函数,当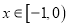 时,
时,  ).
).(1)当
 时,求
时,求 的解析式;
的解析式;(2)若
 ,试判断
,试判断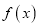 的上单调性,并证明你的结论;
的上单调性,并证明你的结论;(3)是否存在
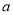 ,使得当
,使得当 时,
时, 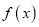 有最大值
有最大值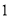 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x3-3ax-1,a≠0.
(1)求f(x)的单调区间;
(2)若f(x)在x=-1处取得极值,直线y=m与y=f(x)的图象有三个不同的交点,求m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,BC边上的中线AD长为3,且BD=2,sinB=
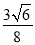 .
.(Ⅰ)求sin∠BAD的值;
(Ⅱ)求AC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设关于θ的方程
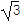 cosθ+sinθ+a=0在区间(0,2π)内有相异的两个实根α、β.
cosθ+sinθ+a=0在区间(0,2π)内有相异的两个实根α、β.(1)求实数a的取值范围;
(2)求α+β的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a是实数,函数f(x)=
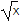 (x-a).
(x-a).(1)求函数f(x)的单调区间;
(2)设g(a)为f(x)在区间[0,2]上的最小值.
①写出g(a)的表达式;
②求a的取值范围,使得-6≤g(a)≤-2.
相关试题

