【题目】已知向量![]() ,
, ![]() ,设函数
,设函数![]() .
.
(1)求函数![]() 的最小正周期;
的最小正周期;
(2)已知![]() 分别为三角形
分别为三角形![]() 的内角对应的三边长,
的内角对应的三边长, ![]() 为锐角,
为锐角, ![]() ,
, ![]() ,且
,且![]() 恰是函数
恰是函数![]() 在
在![]() 上的最大值,求
上的最大值,求![]() 和三角形
和三角形![]() 的面积.
的面积.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() 或
或![]() ,
, ![]() 或
或![]() .
.
【解析】试题分析:本题主要考查平面向量的数量积、二倍角公式、两角和的正弦公式、三角函数、余弦定理、三角形面积等基础知识,意在考查考生的运算求解能力、转化化归想象能力和数形结合能力.第一问,先利用向量的数量积得到![]() 的解析式,利用降幂公式、倍角公式、两角和的正弦公式化简表达式,使之化简成
的解析式,利用降幂公式、倍角公式、两角和的正弦公式化简表达式,使之化简成![]() 的形式,利用
的形式,利用![]() 求函数的周期;第二问,先将
求函数的周期;第二问,先将![]() 代入得到
代入得到![]() 的范围,数形结合得到
的范围,数形结合得到![]() 的最大值,并求出此时的角A,在三角形中利用余弦定理得到边b的值,最后利用
的最大值,并求出此时的角A,在三角形中利用余弦定理得到边b的值,最后利用![]() 求三角形面积.
求三角形面积.
试题解析:(1)![]()
![]()
![]()
![]() 4分
4分
因为![]() ,所以最小正周期
,所以最小正周期![]() . 6分
. 6分
(2)由(1)知![]() ,当
,当![]() 时,
时,![]() .
.
由正弦函数图象可知,当![]() 时,
时, ![]() 取得最大值
取得最大值![]() ,又
,又![]() 为锐角
为锐角
所以![]() . 8分
. 8分
由余弦定理![]() 得
得![]() ,所以
,所以![]() 或
或
![]()
经检验均符合题意. 10分
从而当![]() 时,△
时,△![]() 的面积
的面积![]() ; 11分
; 11分
当![]() 时,
时,![]() . 12分
. 12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a是实数,函数f(x)=
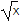 (x-a).
(x-a).(1)求函数f(x)的单调区间;
(2)设g(a)为f(x)在区间[0,2]上的最小值.
①写出g(a)的表达式;
②求a的取值范围,使得-6≤g(a)≤-2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4,且位于x轴上方的点,A到抛物线准线的距离等于5,过A作AB垂直于y轴,垂足为B,OB的中点为M.
(1)求抛物线的方程;
(2)以M为圆心,MB为半径作圆M,当K(m,0)是x轴上一动点时,讨论直线AK与圆M的位置关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4,且位于x轴上方的点,A到抛物线准线的距离等于5,过A作AB垂直于y轴,垂足为B,OB的中点为M.
(1)求抛物线的方程;
(2)以M为圆心,MB为半径作圆M,当K(m,0)是x轴上一动点时,讨论直线AK与圆M的位置关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】同时掷两个骰子,计算:
(1)一共有多少种不同的结果?
(2)其中向上的点数之和是5的结果有多少种?
(3)向上的点数之和是5的概率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a是实数,函数f(x)=
 (x-a).
(x-a).(1)求函数f(x)的单调区间;
(2)设g(a)为f(x)在区间[0,2]上的最小值.
①写出g(a)的表达式;
②求a的取值范围,使得-6≤g(a)≤-2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】比较下列各组中两个值的大小 :
(1)ln0.3,ln2; (2)loga3.1,loga5.2(a>0,且a≠1);
(3)log30.2,log40.2; (4)log3π,logπ3.
相关试题

