【题目】将函数y= ![]() cosx+sinx(x∈R)的图象向左平移m(m>0)个单位长度后,所得到的图象关于y轴对称,则m的最小值是( )
cosx+sinx(x∈R)的图象向左平移m(m>0)个单位长度后,所得到的图象关于y轴对称,则m的最小值是( )
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】B
【解析】解:y= ![]() cosx+sinx=2(
cosx+sinx=2( ![]() cosx+
cosx+ ![]() sinx)=2sin(x+
sinx)=2sin(x+ ![]() ),
),
∴图象向左平移m(m>0)个单位长度得到y=2sin[(x+m)+ ![]() ]=2sin(x+m+
]=2sin(x+m+ ![]() ),
),
∵所得的图象关于y轴对称,
∴m+ ![]() =kπ+
=kπ+ ![]() (k∈Z),
(k∈Z),
则m的最小值为 ![]() .
.
故选B
【考点精析】解答此题的关键在于理解两角和与差的正弦公式的相关知识,掌握两角和与差的正弦公式:![]() ,以及对函数y=Asin(ωx+φ)的图象变换的理解,了解图象上所有点向左(右)平移
,以及对函数y=Asin(ωx+φ)的图象变换的理解,了解图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题正确的个数是( )
①命题“x0∈R,x02+1>3x0”的否定是“x∈R,x2+1≤3x”;
②“函数f(x)=cos2ax﹣sin2ax的最小正周期为π”是“a=1”的必要不充分条件;
③x2+2x≥ax在x∈[1,2]上恒成立(x2+2x)min≥(ax)max在x∈[1,2]上恒成立;
④“平面向量 与
与 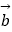 的夹角是钝角”的充分必要条件是“
的夹角是钝角”的充分必要条件是“ 
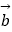 <0”.
<0”.
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=acos2x+(a﹣1)(cosx+1),其中a>0,记f(x)的最大值为A.
(1)求f′(x);
(2)求A;
(3)证明:|f′(x)|≤2A. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
 的不等式
的不等式 的解集为
的解集为 ,则关于
,则关于 的不等式
的不等式 的解集为__________.
的解集为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】[选修4-4:坐标系与参数方程]在直角坐标系xOy中,曲线C1的参数方程为
 (α为参数),以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为ρsin(θ+
(α为参数),以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为ρsin(θ+  )=2
)=2  .
.
(1)写出C1的普通方程和C2的直角坐标方程;
(2)设点P在C1上,点Q在C2上,求|PQ|的最小值及此时P的直角坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】公比为4的等比数列{bn}中,若Tn是数列{bn}的前n项积,则有
 仍成等比数列,且公比为4100;类比上述结论,在公差为3的等差数列{an}中,若Sn是{an}的前n项和,则有________也成等差数列,该等差数列的公差为________.
仍成等比数列,且公比为4100;类比上述结论,在公差为3的等差数列{an}中,若Sn是{an}的前n项和,则有________也成等差数列,该等差数列的公差为________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知过抛物线
 的焦点,斜率为
的焦点,斜率为 的直线交抛物线于
的直线交抛物线于 两点,且
两点,且 .
.(1)求该抛物线的方程;
(2)
 为坐标原点,
为坐标原点, 为抛物线上一点,若
为抛物线上一点,若 ,求
,求 的值.
的值.
相关试题

