【题目】已知过抛物线![]() 的焦点,斜率为
的焦点,斜率为![]() 的直线交抛物线于
的直线交抛物线于![]() 两点,且
两点,且![]() .
.
(1)求该抛物线的方程;
(2) ![]() 为坐标原点,
为坐标原点,![]() 为抛物线上一点,若
为抛物线上一点,若![]() ,求
,求![]() 的值.
的值.
参考答案:
【答案】(1)y2=8x.(2)λ=0,或λ=2.
【解析】试题分析:第一问求抛物线的焦点弦长问题可直接利用焦半径公式,先写出直线的方程,再与抛物线的方程联立方程组,设而不求,利用根与系数关系得出![]() ,然后利用焦半径公式得出焦点弦长公式
,然后利用焦半径公式得出焦点弦长公式![]() ,求出弦长,第二问根据联立方程组解出的A、B两点坐标,和向量的坐标关系表示出点C的坐标,由于点C在抛物线上满足抛物线方程,求出参数值.
,求出弦长,第二问根据联立方程组解出的A、B两点坐标,和向量的坐标关系表示出点C的坐标,由于点C在抛物线上满足抛物线方程,求出参数值.
试题解析:
(1)直线AB的方程是y=2![]() (x-2),与y2=8x联立,消去y得x2-5x+4=0,
(x-2),与y2=8x联立,消去y得x2-5x+4=0,
由根与系数的关系得x1+x2=5.由抛物线定义得|AB|=x1+x2+p=9,
(2)由x2-5x+4=0,得x1=1,x2=4,从而A(1,-2![]() ),B(4,4
),B(4,4![]() ).
).
设![]() =(x3,y3)=(1,-2
=(x3,y3)=(1,-2![]() )+λ(4,4
)+λ(4,4![]() )=(4λ+1,4
)=(4λ+1,4![]() λ-2
λ-2![]() ),
),
又y=8x3,即[2![]() (2λ-1)]2=8(4λ+1),即(2λ-1)2=4λ+1,
(2λ-1)]2=8(4λ+1),即(2λ-1)2=4λ+1,
解得λ=0或λ=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
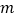 ,
,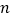 是两条不同直线,
是两条不同直线,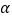 ,
,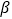 是两个不同平面,则下列命题正确的是 ( )
是两个不同平面,则下列命题正确的是 ( )A. 若
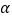 ,
,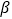 垂直于同一平面,则
垂直于同一平面,则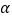 与
与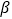 平行
平行B. 若
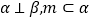 ,则
,则
C. 若
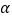 ,
,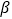 不平行,则在
不平行,则在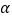 内不存在与
内不存在与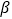 平行的直线
平行的直线D. 若
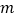 ,
,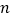 不平行,则
不平行,则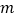 与
与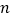 不可能垂直于同一平面
不可能垂直于同一平面 -
科目: 来源: 题型:
查看答案和解析>>【题目】根据市场分析,某蔬菜加工点,当月产量为10吨至25吨时,月生产总成本
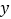 (万元)可以看出月产量
(万元)可以看出月产量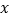 (吨)的二次函数,当月产量为10吨时,月生产成本为20万元,当月产量为15吨时,月生产总成本最低至17.5万元.
(吨)的二次函数,当月产量为10吨时,月生产成本为20万元,当月产量为15吨时,月生产总成本最低至17.5万元.(I)写出月生产总成本
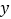 (万元)关于月产量
(万元)关于月产量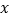 吨的函数关系;
吨的函数关系;(II)已知该产品销售价为每吨1.6万元,那么月产量为多少吨时,可获得最大利润,并求出最大利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (a为常数)的图象与
(a为常数)的图象与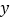 轴交于点
轴交于点 ,曲线
,曲线 在点
在点 处的切线斜率为
处的切线斜率为
(1)求
 的值及函数
的值及函数 的极值;
的极值;(2)证明:当
 时,
时,
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
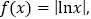
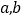 为实数,且
为实数,且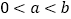 ,
,(I)求方程
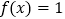 的解;
的解; (II)若
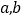 满足
满足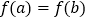 ,求证:①
,求证:①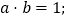 ②
②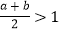 ;
; (III)在(2)的条件下,求证:由关系式
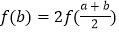 所得到的关于
所得到的关于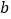 的方程
的方程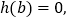 存在
存在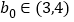 ,使
,使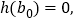
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=2x,g(x)是一次函数,并且点(2,2)在函数f[(g(x)]的图象上,点(2,5)在函数g[f(x)]的图象上,则g(x)的解析式为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图给出了一个程序框图,其作用是输入x的值,输出相应的y值.若要使输入的x值与输出的y值相等,则这样的x值有( )
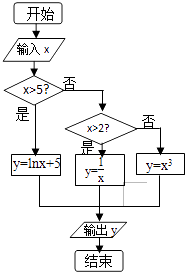
A.1个
B.2个
C.3个
D.4个
相关试题

