【题目】如图,在多面体![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的正方形,四边形
的正方形,四边形![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() 和
和![]() 分别是
分别是![]() 和
和![]() 的中点.
的中点.
(Ⅰ)求证: ![]() 平面
平面![]() .
.
(Ⅱ)求证:平面![]() 平面
平面![]() .
.
(Ⅲ)求多面体![]() 的体积.
的体积.
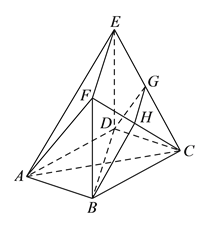
参考答案:
【答案】(1)见解析(2)见解析(3)8
【解析】试题分析:(1)由面面垂直性质定理得![]() 平面
平面![]() ,即得
,即得![]() ,而由正方形性质得
,而由正方形性质得![]() ,所以由线面垂直判定定理得
,所以由线面垂直判定定理得![]() 平面
平面![]() .(2)设
.(2)设![]() 与
与![]() 相交于
相交于![]() 点,由三角形中位线性质易得
点,由三角形中位线性质易得![]() ,
, ![]() ,再由线面平行判定定理以及面面平行判定定理得结论(3)即求两个四棱锥
,再由线面平行判定定理以及面面平行判定定理得结论(3)即求两个四棱锥![]() 与棱锥
与棱锥![]() 体积之和,而AC为高,根据锥体体积公式求体积
体积之和,而AC为高,根据锥体体积公式求体积
试题解析:(Ⅰ)证明:∵在正方形![]() 中,
中,
![]() ,
,
∵平面![]() 平面
平面![]() ,
,
且平面![]() 平面
平面![]() ,
,
在矩形![]() 中,
中,
![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() ,
,
∵![]() 点,
点,
![]() 、
、![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(Ⅱ)设![]() 与
与![]() 相交于
相交于![]() 点,
点,
∵![]() 、
、![]() 是
是![]() 、
、![]() 中点,
中点,
∴![]() ,
,
又∵![]() 、
、![]() 是
是![]() 、
、![]() 中点,
中点,
∴![]() ,
,
∵![]() 点,
点,
![]() 点,
点,
![]() 、
、![]() 平面
平面![]() ,
,
![]() 、
、![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(Ⅲ)将多面体![]() 分割为
分割为
棱锥![]() 与棱锥
与棱锥![]() ,
,
∵![]() 、
、![]() 到平面
到平面![]() 的距离均为
的距离均为![]() 的长度,
的长度,
∴![]()
![]()
![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】国家规定,中小学生每天在校体育活动时间不低于1小时,为了解这项政策的落实情况,有关部门就“你某天在校体育活动时间是多少”的问题,在某校随机抽查了部分学生,再根据活动时间t(小时)进行分组(A组:t<0.5,B组:0.5≤t≤1,C组:1≤t<1.5,D组:t≥1.5),绘制成如下两幅不完整统计图,请根据图中信息回答问题:

(1)此次抽查的学生数为人;
(2)补全条形统计图;
(3)从抽查的学生中随机询问一名学生,该生当天在校体育活动时间低于1小时的概率是
(4)若当天在校学生数为1200人,请估计在当天达到国家规定体育活动时间的学生有人. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是将一正方体货物沿坡面AB装进汽车货厢的平面示意图.已知长方体货厢的高度BC为
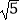 米,tanA=
米,tanA=  ,现把图中的货物继续往前平移,当货物顶点D与C重合时,仍可把货物放平装进货厢,求BD的长.(结果保留根号)
,现把图中的货物继续往前平移,当货物顶点D与C重合时,仍可把货物放平装进货厢,求BD的长.(结果保留根号)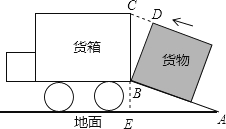
-
科目: 来源: 题型:
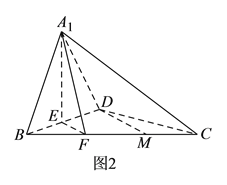
查看答案和解析>>【题目】如图
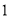 ,在
,在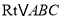 中,
中, 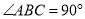 ,
, 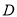 为
为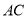 中点,
中点, 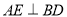 于
于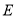 (不同于点
(不同于点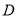 ),延长
),延长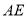 交
交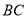 于
于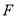 ,将
,将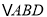 沿
沿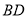 折起,得到三棱锥
折起,得到三棱锥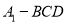 ,如图
,如图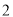 所示.
所示.(Ⅰ)若
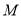 是
是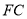 的中点,求证:直线
的中点,求证:直线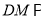 平面
平面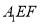 .
.(Ⅱ)求证:
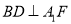 .
.(Ⅲ)若平面
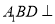 平面
平面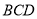 ,试判断直线
,试判断直线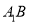 与直线
与直线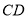 能否垂直?请说明理由.
能否垂直?请说明理由.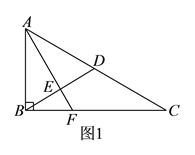
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校准备组织师生共60人,从南靖乘动车前往厦门参加夏令营活动,动车票价格如表所示:(教师按成人票价购买,学生按学生票价购买).
运行区间
成人票价(元/张)
学生票价(元/张)
出发站
终点站
一等座
二等座
二等座
南靖
厦门
26
22
16
若师生均购买二等座票,则共需1020元.
(1)参加活动的教师有人,学生有人;
(2)由于部分教师需提早前往做准备工作,这部分教师均购买一等座票,而后续前往的教师和学生均购买二等座票.设提早前往的教师有x人,购买一、二等座票全部费用为y元.
①求y关于x的函数关系式;
②若购买一、二等座票全部费用不多于1032元,则提早前往的教师最多只能多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,点E在⊙O上,C为
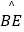 的中点,过点C作直线CD⊥AE于D,连接AC、BC.
的中点,过点C作直线CD⊥AE于D,连接AC、BC.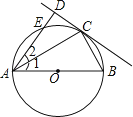
(1)试判断直线CD与⊙O的位置关系,并说明理由;
(2)若AD=2,AC=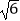 ,求AB的长.
,求AB的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某种药种植基地有两处种植区的药材需在下周一、周二两天内采摘完毕,基地员工一天可以完成一处种植区的采摘,由于下雨会影响药材的收益,若基地收益如下表所示:已知下周一和下周二无雨的概率相同且为
 ,两天是否下雨互不影响,若两天都下雨的概率为
,两天是否下雨互不影响,若两天都下雨的概率为

(1)求
 及基地的预期收益;
及基地的预期收益;(2)若该基地额外聘请工人,可在周一当天完成全部采摘任务,若周一无雨时收益为
 万元,有雨时收益为
万元,有雨时收益为 万元,且额外聘请工人的成本为
万元,且额外聘请工人的成本为 元,问该基地是否应该额外聘请工人,请说明理由.
元,问该基地是否应该额外聘请工人,请说明理由.
相关试题

