【题目】某种药种植基地有两处种植区的药材需在下周一、周二两天内采摘完毕,基地员工一天可以完成一处种植区的采摘,由于下雨会影响药材的收益,若基地收益如下表所示:已知下周一和下周二无雨的概率相同且为![]() ,两天是否下雨互不影响,若两天都下雨的概率为
,两天是否下雨互不影响,若两天都下雨的概率为![]()

(1)求![]() 及基地的预期收益;
及基地的预期收益;
(2)若该基地额外聘请工人,可在周一当天完成全部采摘任务,若周一无雨时收益为![]() 万元,有雨时收益为
万元,有雨时收益为![]() 万元,且额外聘请工人的成本为
万元,且额外聘请工人的成本为![]() 元,问该基地是否应该额外聘请工人,请说明理由.
元,问该基地是否应该额外聘请工人,请说明理由.
参考答案:
【答案】(1) ![]() 基地的预期收益为9.16万元;(2)见解析.
基地的预期收益为9.16万元;(2)见解析.
【解析】试题分析:
(1)由于两天下雨是相互独立的,因此两天都下雨的概率是![]() ,由此可得
,由此可得![]() ;该基地收益
;该基地收益![]() 的可能取值为10,8, 5(单位:万元),分别计算要概率,然后列出概率分布列,计算出数学期望.(2)该基地额外聘请工人的预期收益绝对值计算易得,现第(1)小题,比较两个预期值可得.
的可能取值为10,8, 5(单位:万元),分别计算要概率,然后列出概率分布列,计算出数学期望.(2)该基地额外聘请工人的预期收益绝对值计算易得,现第(1)小题,比较两个预期值可得.
试题解析:
(1) 两天都下雨的概率为![]() ,解得
,解得![]() .
.
该基地收益![]() 的可能取值为10,8, 5。(单位:万元)则:
的可能取值为10,8, 5。(单位:万元)则:
![]() ,
, ![]() ,
, ![]()
所以该基地收益![]() 的分布列为:
的分布列为:
| 10 | 8 | 5 |
| 0.64 | 0.32 | 0.04 |
则该基地的预期收益![]() (万元)
(万元)
所以,基地的预期收益为9.16万元
⑵设基地额外聘请工人时的收益为![]() 万元,则其预期收益:
万元,则其预期收益:
![]() (万元)
(万元)
此时![]() ,所以该基地应该外聘工人.
,所以该基地应该外聘工人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在多面体
 中,底面
中,底面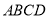 是边长为
是边长为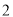 的正方形,四边形
的正方形,四边形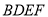 是矩形,平面
是矩形,平面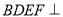 平面
平面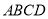 ,
, 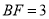 ,
, 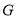 和
和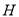 分别是
分别是 和
和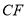 的中点.
的中点.(Ⅰ)求证:
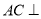 平面
平面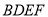 .
.(Ⅱ)求证:平面
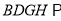 平面
平面 .
.(Ⅲ)求多面体
 的体积.
的体积.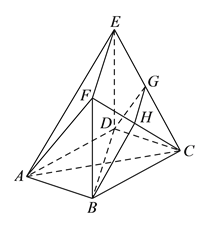
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校准备组织师生共60人,从南靖乘动车前往厦门参加夏令营活动,动车票价格如表所示:(教师按成人票价购买,学生按学生票价购买).
运行区间
成人票价(元/张)
学生票价(元/张)
出发站
终点站
一等座
二等座
二等座
南靖
厦门
26
22
16
若师生均购买二等座票,则共需1020元.
(1)参加活动的教师有人,学生有人;
(2)由于部分教师需提早前往做准备工作,这部分教师均购买一等座票,而后续前往的教师和学生均购买二等座票.设提早前往的教师有x人,购买一、二等座票全部费用为y元.
①求y关于x的函数关系式;
②若购买一、二等座票全部费用不多于1032元,则提早前往的教师最多只能多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,点E在⊙O上,C为
 的中点,过点C作直线CD⊥AE于D,连接AC、BC.
的中点,过点C作直线CD⊥AE于D,连接AC、BC.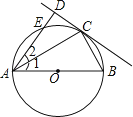
(1)试判断直线CD与⊙O的位置关系,并说明理由;
(2)若AD=2,AC=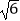 ,求AB的长.
,求AB的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2+bx+c与x轴交于点A和点B(3,0),与y轴交于点C(0,3).
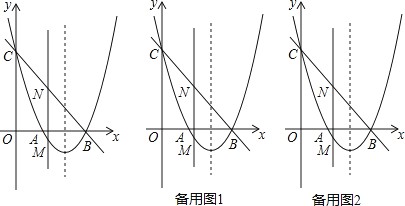
(1)求抛物线的解析式;
(2)若点M是抛物线在x轴下方上的动点,过点M作MN∥y轴交直线BC于点N,求线段MN的最大值;
(3)在(2)的条件下,当MN取得最大值时,在抛物线的对称轴l上是否存在点P,使△PBN是等腰三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】现有正方形ABCD和一个以O为直角顶点的三角板,移动三角板,使三角板两直角边所在直线分别与直线BC、CD交于点M、N.

(1)如图1,若点O与点A重合,则OM与ON的数量关系是
(2)如图2,若点O在正方形的中心(即两对角线交点),则(1)中的结论是否仍然成立?请说明理由;
(3)如图3,若点O在正方形的内部(含边界),当OM=ON时,请探究点O在移动过程中可形成什么图形?
(4)如图4,是点O在正方形外部的一种情况.当OM=ON时,请你就“点O的位置在各种情况下(含外部)移动所形成的图形”提出一个正确的结论.(不必说明) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,底面
中,底面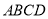 是边长为
是边长为 的正方形,侧面
的正方形,侧面
底面
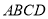 ,且
,且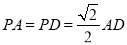 ,
,  、
、 分别为
分别为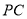 、
、 的中点.
的中点.
(1)求证:
 平面
平面 ;
;(2)求证:面
 平面
平面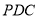 ;
;(3)在线段
 上是否存在点
上是否存在点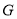 ,使得二面角
,使得二面角 的余弦值为
的余弦值为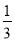 ?说明理由.
?说明理由.
相关试题

