【题目】如图是正四面体的平面展开图,G,H,M,N分别为DE,BE,EF,EC的中点,在这个正四面体中,
①GH与EF平行;②BD与MN为异面直线;③GH与MN成60°角;④DE与MN垂直.以上四个命题中,正确命题的序号是 . 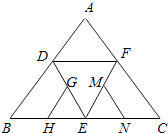
参考答案:
【答案】②③④
【解析】解:将正四面体的平面展开图复原为正四面体A(B、C)﹣DEF,如图: 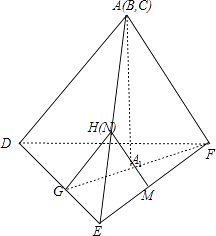
对于①,G、H分别为DE、BE的中点,则GH∥AD,而AD与EF异面,故GH与EF不平行,故①错误;
对于②,BD与MN为异面直线,正确(假设BD与MN共面,则A、D、E、F四点共面,与ADEF为正四面体矛盾,故假设不成立,故BD与MN异面);
对于③,依题意,GH∥AD,MN∥AF,∠DAF=60°,故GH与MN成60°角,故③正确;
对于④,连接GF,A点在平面DEF的射影A1在GF上,∴DE⊥平面AGF,DE⊥AF,
而AF∥MN,∴DE与MN垂直,故④正确.
综上所述,正确命题的序号是②③④,
故答案为:②③④.
正四面体的平面展开图复原为正四面体A(B、C)﹣DEF,①,依题意,GH∥AD,而AD与EF异面,从而可判断GH与EF不平行;②,假设BD与MN共面,可得A、D、E、F四点共面,导出矛盾,从而可否定假设,肯定BD与MN为异面直线;③,依题意知,GH∥AD,MN∥AF,∠DAF=60°,于是可判断GH与MN成60°角;④,连接GF,那么A点在平面DEF的射影肯定在GF上,通过线面垂直得到线线垂直.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若不等式|2x﹣1|﹣|x+a|≥a对任意的实数x恒成立,则实数a的取值范围是( )
A.(﹣∞,﹣ ]
]
B.(﹣ ,﹣
,﹣  ]
]
C.(﹣ ,0)
,0)
D.(﹣∞,﹣ ]
] -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=a﹣
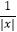 ,
,
(1)若x∈[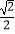 ,+∞),①判断函数g(x)=f(x)﹣2x的单调性并加以证明;②如果f(x)≤2x恒成立,求a的取值范围;
,+∞),①判断函数g(x)=f(x)﹣2x的单调性并加以证明;②如果f(x)≤2x恒成立,求a的取值范围;
(2)若总存在m,n使得当x∈[m,n]时,恰有f(x)∈[2m,2n],求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数g(x)=ex , f(x)=
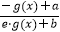 ,f(x)是定义在R上的奇函数.
,f(x)是定义在R上的奇函数.
(1)求a,b的值;
(2)若关于t的方程f(2t2﹣mt)+f(1﹣t2)=0有两个根α、β,且α>0,1<β<2,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的不等式ax2﹣|x+1|+3a≥0的解集为(﹣∞,+∞),则实数a的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的不等式ax2+bx+c>0的解集为{x|﹣1<x<2},求不等式a(x2+1)+b(x﹣1)+c>2ax的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从装有大小相同的2个红球和6个白球的袋子中,每摸出2个球为一次试验,直到摸出的球中有红球(不放回),则试验结束.
(1)求第一次试验恰摸到一个红球和一个白球概率;
(2)记试验次数为
 ,求
,求 的分布列及数学期望
的分布列及数学期望 .
.
相关试题

