【题目】设函数f(x)=a﹣ ![]() ,
,
(1)若x∈[ ![]() ,+∞),①判断函数g(x)=f(x)﹣2x的单调性并加以证明;②如果f(x)≤2x恒成立,求a的取值范围;
,+∞),①判断函数g(x)=f(x)﹣2x的单调性并加以证明;②如果f(x)≤2x恒成立,求a的取值范围;
(2)若总存在m,n使得当x∈[m,n]时,恰有f(x)∈[2m,2n],求a的取值范围.
参考答案:
【答案】
(1)解:①x∈[ ![]() ,+∞)时,g(x)=f(x)﹣2x=a﹣
,+∞)时,g(x)=f(x)﹣2x=a﹣ ![]() .
.
任取 ![]() ,
,
![]() =
= ![]() .
.
∵ ![]() ,∴x2﹣x10,x1x2>0.
,∴x2﹣x10,x1x2>0.
∴g(x1)﹣g(x2)<0,g(x1)<g(x2).
∴g(x)在[ ![]() ,+∞)上单调递减.
,+∞)上单调递减.
②f(x)≤2xg(x)≤0,∵g(x)在[ ![]() ,+∞)上单调递减,
,+∞)上单调递减,
∴ ![]() ,∴
,∴ ![]()
(2)解:∵f(x)=a﹣ ![]() 的定义域为(﹣∞,0)∪(0,+∞),∴mn>0
的定义域为(﹣∞,0)∪(0,+∞),∴mn>0
若n>m>0,则 ![]() ,且在[m,n]上递增,∴
,且在[m,n]上递增,∴ ![]() ,∴
,∴ 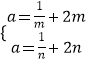 .
.
∴m,n是 ![]() 的两个根,即2x2﹣ax+1=0的两个根,
的两个根,即2x2﹣ax+1=0的两个根,
∴ 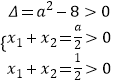 ,解得
,解得 ![]() .
.
若m<n<0,则f(x)=a+ ![]() ,且在[m,n]上递减,
,且在[m,n]上递减,
∴ ![]() ,∴
,∴ 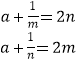 ,相减得:mn=
,相减得:mn= ![]() ,代回得:a=0.
,代回得:a=0.
综上所得:a的取值范围是( ![]() )∪{0}
)∪{0}
【解析】(1)①把f(x)的解析式代入后,直接利用函数的单调性的定义证明;②由①中的单调性求出g(x)的最大值,由最大值小于等于0求解a的范围;(2)求出函数的定义域,然后分m,n同正和同负两种情况分析,借助于函数的单调性的方程组,然后再转化为方程的根进行分析.
【考点精析】解答此题的关键在于理解函数单调性的判断方法的相关知识,掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在△ABC中,角A,B,C的对边分别是a,b,c,向量m=(2b,1),n=(2a-c,cos C),且m∥n.(1)若b2=ac,试判断△ABC的形状;(2)求y=1-
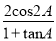 的值域.
的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱ABC﹣A1B1C1中,底面为正三角形,侧棱垂直底面,AB=4,AA1=6,若E,F分别是棱BB1 , CC1上的点,且BE=B1E,C1F=
 CC1 , 则异面直线A1E与AF所成角的余弦值为( )
CC1 , 则异面直线A1E与AF所成角的余弦值为( ) 
A.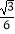
B.
C.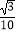
D.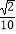
-
科目: 来源: 题型:
查看答案和解析>>【题目】若不等式|2x﹣1|﹣|x+a|≥a对任意的实数x恒成立,则实数a的取值范围是( )
A.(﹣∞,﹣ ]
]
B.(﹣ ,﹣
,﹣  ]
]
C.(﹣ ,0)
,0)
D.(﹣∞,﹣ ]
] -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数g(x)=ex , f(x)=
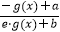 ,f(x)是定义在R上的奇函数.
,f(x)是定义在R上的奇函数.
(1)求a,b的值;
(2)若关于t的方程f(2t2﹣mt)+f(1﹣t2)=0有两个根α、β,且α>0,1<β<2,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是正四面体的平面展开图,G,H,M,N分别为DE,BE,EF,EC的中点,在这个正四面体中,
①GH与EF平行;②BD与MN为异面直线;③GH与MN成60°角;④DE与MN垂直.以上四个命题中,正确命题的序号是 .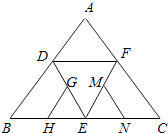
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的不等式ax2﹣|x+1|+3a≥0的解集为(﹣∞,+∞),则实数a的取值范围是 .
相关试题

