【题目】关于x的不等式ax2﹣|x+1|+3a≥0的解集为(﹣∞,+∞),则实数a的取值范围是 .
参考答案:
【答案】[ ![]() ,+∞)
,+∞)
【解析】解:不等式ax2﹣|x+1|+3a≥0,
则a(x2+3)≥|x+1|,
即a≥ ![]() ,
,
设t=x+1,则x=t﹣1,
则不等式a≥ ![]() 等价为a≥
等价为a≥ ![]() =
= ![]() =
= ![]() >0
>0
即a>0,
设f(t)= ![]() ,
,
当|t|=0,即x=﹣1时,不等式等价为a+3a=4a≥0,此时满足条件,
当t>0,f(t)= ![]() =
= 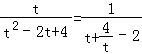
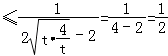 ,当且仅当t=
,当且仅当t= ![]() ,
,
即t=2,即x=1时取等号.
当t<0,f(t)= ![]() =
= 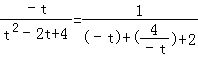 ≤
≤ 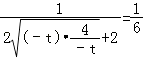 ,
,
当且仅当﹣t=﹣ ![]() ,
,
∴t=﹣2,即x=﹣3时取等号.
∴当x=1,即t=2时,fmax(t)= ![]() =
= ![]() ,
,
∴要使a≥ ![]() 恒成立,则a
恒成立,则a ![]() ,
,
方法2:由不等式ax2﹣|x+1|+3a≥0,
则a(x2+3)≥|x+1|,
∴要使不等式的解集是(﹣∞,+∞),则a>0,
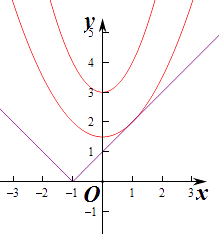
作出y=a(x2+3)和y=|x+1|的图象,
由图象知只要当x>﹣1时,直线y═|x+1|=x+1与y=a(x2+3)相切或相离即可,
此时不等式ax2﹣|x+1|+3a≥0等价为不等式ax2﹣x﹣1+3a≥0,
对应的判别式△=1﹣4a(3a﹣1)≤0,
即﹣12a2+4a+1≤0,
即12a2﹣4a﹣1≥0,
(2a﹣1)(6a+1)≥0,
解得a≥ ![]() 或a≤﹣
或a≤﹣ ![]() (舍),
(舍),
故答案为:[ ![]() ,+∞)
,+∞)
将不等式恒成立进行参数分类得到a≥ ![]() ,利用换元法将不等式转化为基本不等式的性质,根据基本不等式的性质求出
,利用换元法将不等式转化为基本不等式的性质,根据基本不等式的性质求出 ![]() 的最大值即可得到结论.
的最大值即可得到结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=a﹣
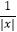 ,
,
(1)若x∈[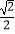 ,+∞),①判断函数g(x)=f(x)﹣2x的单调性并加以证明;②如果f(x)≤2x恒成立,求a的取值范围;
,+∞),①判断函数g(x)=f(x)﹣2x的单调性并加以证明;②如果f(x)≤2x恒成立,求a的取值范围;
(2)若总存在m,n使得当x∈[m,n]时,恰有f(x)∈[2m,2n],求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数g(x)=ex , f(x)=
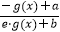 ,f(x)是定义在R上的奇函数.
,f(x)是定义在R上的奇函数.
(1)求a,b的值;
(2)若关于t的方程f(2t2﹣mt)+f(1﹣t2)=0有两个根α、β,且α>0,1<β<2,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是正四面体的平面展开图,G,H,M,N分别为DE,BE,EF,EC的中点,在这个正四面体中,
①GH与EF平行;②BD与MN为异面直线;③GH与MN成60°角;④DE与MN垂直.以上四个命题中,正确命题的序号是 .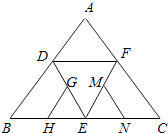
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的不等式ax2+bx+c>0的解集为{x|﹣1<x<2},求不等式a(x2+1)+b(x﹣1)+c>2ax的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从装有大小相同的2个红球和6个白球的袋子中,每摸出2个球为一次试验,直到摸出的球中有红球(不放回),则试验结束.
(1)求第一次试验恰摸到一个红球和一个白球概率;
(2)记试验次数为
 ,求
,求 的分布列及数学期望
的分布列及数学期望 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 :
: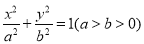 的一个焦点与抛物线
的一个焦点与抛物线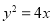 的焦点相同,
的焦点相同, ,
,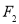 为椭圆的左、右焦点.
为椭圆的左、右焦点.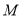 为椭圆上任意一点,△
为椭圆上任意一点,△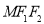 面积的最大值为1.
面积的最大值为1.(1)求椭圆
 的方程;
的方程;(2)直线
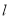 :
:
 交椭圆
交椭圆 于
于 ,
,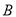 两点.
两点.(i)若直线
 与
与 的斜率分别为
的斜率分别为 ,
, ,且
,且 ,求证:直线
,求证:直线 过定点,并求出该定点的坐标;
过定点,并求出该定点的坐标;(ii)若直线
 的斜率时直线
的斜率时直线 ,
, 斜率的等比中项,求△
斜率的等比中项,求△ 面积的取值范围.
面积的取值范围.
相关试题

