【题目】已知数列{an}的前n项和为Sn , 且a1=1,Sn+1﹣2Sn=1(n∈N*).
(1)求数列{an}的通项公式;
(2)若数列{bn}满足bn=n+ ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
参考答案:
【答案】
(1)解:a1=1,Sn+1﹣2Sn=1,
即为Sn+1+1=2(Sn+1),
即有数列{Sn+1}是以S1+1=2,2为公比的等比数列,
则Sn+1=22n﹣1=2n,
即Sn=2n﹣1,n∈N*,
当n≥2时,an=Sn﹣Sn﹣1=2n﹣1﹣(2n﹣1﹣1)=2n﹣1,
上式对n=1也成立,
则数列{an}的通项公式为an=2n﹣1,n∈N*
(2)解:bn=n+ ![]() =n+n(
=n+n( ![]() )n﹣1,
)n﹣1,
前n项和Tn=(1+2+3+…+n)+[11+2( ![]() )+3(
)+3( ![]() )2+…+n(
)2+…+n( ![]() )n﹣1],
)n﹣1],
设Mn=11+2( ![]() )+3(
)+3( ![]() )2+…+n(
)2+…+n( ![]() )n﹣1,
)n﹣1,
![]() Mn=1
Mn=1 ![]() +2(
+2( ![]() )2+3(
)2+3( ![]() )3+…+n(
)3+…+n( ![]() )n,
)n,
相减可得, ![]() Mn=1+
Mn=1+ ![]() +(
+( ![]() )2+(
)2+( ![]() )3+…+(
)3+…+( ![]() )n﹣1﹣n(
)n﹣1﹣n( ![]() )n
)n
= ![]() ﹣n(
﹣n( ![]() )n,
)n,
化简可得Mn=4﹣(n+2)( ![]() )n﹣1,
)n﹣1,
则Tn= ![]() n(n+1)+4﹣(n+2)(
n(n+1)+4﹣(n+2)( ![]() )n﹣1
)n﹣1
【解析】(1)由题意可得Sn+1+1=2(Sn+1),即有数列{Sn+1}是以S1+1=2,2为公比的等比数列,运用等比数列的通项公式和数列的递推式,可得所求通项公式;(2)求出bn=n+ ![]() =n+n(
=n+n( ![]() )n﹣1 , 运用数列的求和方法:分组求和和错位相减法,结合等差数列和等比数列的求和公式,化简计算即可得到所求和.
)n﹣1 , 运用数列的求和方法:分组求和和错位相减法,结合等差数列和等比数列的求和公式,化简计算即可得到所求和.
【考点精析】认真审题,首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系 ),还要掌握数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式)的相关知识才是答题的关键.
),还要掌握数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
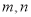 是空间两条直线,
是空间两条直线, 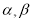 是空间两个平面,则下列命题中不正确的是( )
是空间两个平面,则下列命题中不正确的是( )A. 当
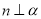 时,“
时,“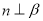 ”是“
”是“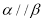 ”的充要条件
”的充要条件B. 当
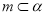 时,“
时,“ ”是“
”是“ ”的充分不必要条件
”的充分不必要条件C. 当
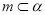 时,“
时,“ ”是“
”是“ ”的必要不充分条件
”的必要不充分条件D. 当
 时,“
时,“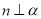 ”是“
”是“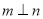 ”的充分不必要条件
”的充分不必要条件 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
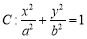
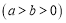 的焦距为2,离心率为
的焦距为2,离心率为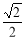 ,
,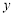 轴上一点
轴上一点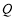 的坐标为
的坐标为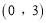 .
.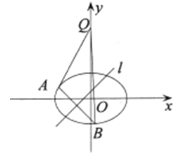
(Ⅰ)求该椭圆的方程;
(Ⅱ)若对于直线
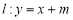 ,椭圆
,椭圆 上总存在不同的两点
上总存在不同的两点 与
与 关于直线
关于直线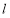 对称,且
对称,且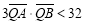 ,求
,求实数
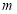 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,射线y=x(x≥0)和y=0(x≥0)上分别依次有点A1、A2 , …,An , …,和点B1 , B2 , …,Bn…,其中
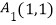 ,
, 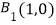 ,
, 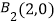 .且
.且 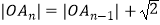 ,
, 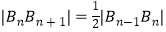 (n=2,3,4…).
(n=2,3,4…). 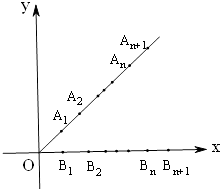
(1)用n表示|OAn|及点An的坐标;
(2)用n表示|BnBn+1|及点Bn的坐标;
(3)写出四边形AnAn+1Bn+1Bn的面积关于n的表达式S(n),并求S(n)的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个命题:
①经过定点P0(x0 , y0)的直线都可以用方程y﹣y0=k(x﹣x0)表示;
②经过定点A(0,b)的直线都可以用方程y=kx+b表示;
③不经过原点的直线都可以用方程 +
+  =1表示;
=1表示;
④经过任意两个不同的 点P1(x1 , y1)、P2(x2 , y2)的直线都可以用方程(y﹣y1)(x2﹣x1)=(x﹣x1)(y2﹣y1)表示;
其中真命题的个数为( )
A.0
B.1
C.2
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是平行四边形ABCD所在平面外一点,E是PD的中点.

(1)求证:PB∥平面EAC;
(2)若M是CD上异于C、D的点.连结PM交CE于G,连结BM交AC于H,求证:GH∥PB. -
科目: 来源: 题型:
查看答案和解析>>【题目】设fk(n)为关于n的k(k∈N)次多项式.数列{an}的首项a1=1,前n项和为Sn . 对于任意的正整数n,an+Sn=fk(n)都成立. (Ⅰ)若k=0,求证:数列{an}是等比数列;
(Ⅱ)试确定所有的自然数k,使得数列{an}能成等差数列.
相关试题

