【题目】下列四个命题:
①经过定点P0(x0 , y0)的直线都可以用方程y﹣y0=k(x﹣x0)表示;
②经过定点A(0,b)的直线都可以用方程y=kx+b表示;
③不经过原点的直线都可以用方程 ![]() +
+ ![]() =1表示;
=1表示;
④经过任意两个不同的 点P1(x1 , y1)、P2(x2 , y2)的直线都可以用方程(y﹣y1)(x2﹣x1)=(x﹣x1)(y2﹣y1)表示;
其中真命题的个数为( )
A.0
B.1
C.2
D.3
参考答案:
【答案】B
【解析】解:①,过点P0(x0 , y0)且垂直于x轴的直线不能用方程y﹣y0=k(x﹣x0)表示,故①错误;②,经过定点A(0,b)且垂直于x轴的直线不能用不能用方程y=kx+b表示,故②错误;
③,垂直于两坐标轴的直线不能用方程 ![]() +
+ ![]() =1表示,故③错误;
=1表示,故③错误;
④,当两个不同的点P1(x1 , y1)、P2(x2 , y2)的连线不垂直于坐标轴时,直线方程为 ![]() ,
,
化为(y﹣y1)(x2﹣x1)=(x﹣x1)(y2﹣y1)后包含两点连线垂直于坐标轴,∴经过任意两个不同的点P1(x1 , y1)、P2(x2 , y2)的直线都可以用方程(y﹣y1)(x2﹣x1)=(x﹣x1)(y2﹣y1)表示,故④正确.
∴正确命题的个数是1个.
故选:B.
【考点精析】根据题目的已知条件,利用命题的真假判断与应用的相关知识可以得到问题的答案,需要掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
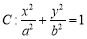
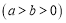 的焦距为2,离心率为
的焦距为2,离心率为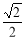 ,
,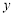 轴上一点
轴上一点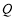 的坐标为
的坐标为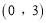 .
.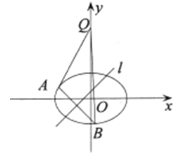
(Ⅰ)求该椭圆的方程;
(Ⅱ)若对于直线
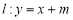 ,椭圆
,椭圆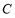 上总存在不同的两点
上总存在不同的两点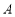 与
与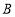 关于直线
关于直线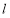 对称,且
对称,且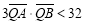 ,求
,求实数
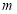 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,射线y=x(x≥0)和y=0(x≥0)上分别依次有点A1、A2 , …,An , …,和点B1 , B2 , …,Bn…,其中
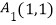 ,
, 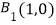 ,
, 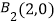 .且
.且 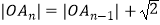 ,
, 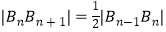 (n=2,3,4…).
(n=2,3,4…). 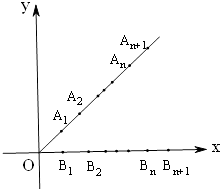
(1)用n表示|OAn|及点An的坐标;
(2)用n表示|BnBn+1|及点Bn的坐标;
(3)写出四边形AnAn+1Bn+1Bn的面积关于n的表达式S(n),并求S(n)的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和为Sn , 且a1=1,Sn+1﹣2Sn=1(n∈N*).
(1)求数列{an}的通项公式;
(2)若数列{bn}满足bn=n+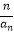 ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是平行四边形ABCD所在平面外一点,E是PD的中点.

(1)求证:PB∥平面EAC;
(2)若M是CD上异于C、D的点.连结PM交CE于G,连结BM交AC于H,求证:GH∥PB. -
科目: 来源: 题型:
查看答案和解析>>【题目】设fk(n)为关于n的k(k∈N)次多项式.数列{an}的首项a1=1,前n项和为Sn . 对于任意的正整数n,an+Sn=fk(n)都成立. (Ⅰ)若k=0,求证:数列{an}是等比数列;
(Ⅱ)试确定所有的自然数k,使得数列{an}能成等差数列. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一次歌手大奖赛上,七位评委为歌手打出的分数如下:9.4,8.4,9.4,9.9,9.6,9.4,9.7,去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为( )
A.9.4,0.484
B.9.4,0.016
C.9.5,0.04
D.9.5,0.016
相关试题

