【题目】已知函数f(x)=cos2x+2sin2x+2sinx.
(Ⅰ)将函数f(2x)的图象向右平移 ![]() 个单位得到函数g(x)的图象,若x∈[
个单位得到函数g(x)的图象,若x∈[ ![]() ,
, ![]() ],求函数g(x)的值域;
],求函数g(x)的值域;
(Ⅱ)已知a,b,c分别为△ABC中角A,B,C的对边,且满足f(A)= ![]() +1,A∈(0,
+1,A∈(0, ![]() ),a=2
),a=2 ![]() ,b=2,求△ABC的面积.
,b=2,求△ABC的面积.
参考答案:
【答案】解:(Ⅰ)因为f(x)=cos2x+2sin2x+2sinx=cosx2﹣sinx2+2sin2x+2sinx=cosx2+sinx2+2sinx=1+2sinx,
即f(2x)=1+2sin2x,
∵函数f(2x)的图象向右平移 ![]() 个单位得到函数g(x)的图象,
个单位得到函数g(x)的图象,
∴ ![]() ,∵
,∵ ![]() ,∴2x﹣
,∴2x﹣ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],
], ![]() ,∴g(x)∈[0,3],
,∴g(x)∈[0,3],
所以函数g(x)的值域为[0,3].
(Ⅱ)解:∵ ![]() ,∴
,∴ ![]() ;因为
;因为 ![]() ,∴
,∴ ![]() .
.
又 ![]() ,
, ![]() ,b=2,∴c=4.
,b=2,∴c=4.
所以,△ABC面积 ![]()
【解析】(Ⅰ)利用三角恒等变换化简函数f(x)的解析式,再利用函数y=Asin(ωx+φ)的图象变换规律,求得g(x)的解析式,利用正弦函数的定义域和值域,求得数g(x)的值域.(Ⅱ)先求得cosA的值,利用余弦定理求得c的值,可得△ABC的面积.
【考点精析】利用函数y=Asin(ωx+φ)的图象变换和余弦定理的定义对题目进行判断即可得到答案,需要熟知图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象;余弦定理:
的图象;余弦定理:![]() ;
;![]() ;
;![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的各项均为正整数,其前n项和为Sn , an+1=
 ,若S3=10,则S180=( )
,若S3=10,则S180=( )
A.600或900
B.900或560
C.900
D.600 -
科目: 来源: 题型:
查看答案和解析>>【题目】定义在区间D上的函数f(x)和g(x),如果对任意x∈D,都有|f(x)﹣g(x)|≤1成立,则称f(x)在区间D上可被g(x)替代,D称为“替代区间”.给出以下问题:
①f(x)=x2+1在区间(﹣∞,+∞)上可被g(x)=x2+ 替代;
替代;
②如果f(x)=lnx在区间[1,e]可被g(x)=x﹣b替代,则﹣2≤b≤2;
③设f(x)=lg(ax2+x)(x∈D1),g(x)=sinx(x∈D1),则存在实数a(a≠0)及区间D1 , D2 , 使得f(x)在区间D1∩D2上被g(x)替代.
其中真命题是( )
A.①②③
B.②③
C.①
D.①② -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A,B是椭圆
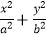 =1和双曲线
=1和双曲线 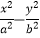 =1的公共顶点,其中a>b>0,P是双曲线上的动点,M是椭圆上的动点(P,M都异于A,B),且满足
=1的公共顶点,其中a>b>0,P是双曲线上的动点,M是椭圆上的动点(P,M都异于A,B),且满足 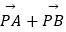 =λ(
=λ( 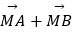 )(λ∈R),设直线AP,BP,AM,BM的斜率分别为k1 , k2 , k3 , k4 , 若k1+k2=
)(λ∈R),设直线AP,BP,AM,BM的斜率分别为k1 , k2 , k3 , k4 , 若k1+k2= 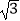 ,则k3+k4= .
,则k3+k4= . -
科目: 来源: 题型:
查看答案和解析>>【题目】某地区2007年至2013年农村居民家庭纯收入
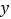 (单位:千元)的数据如下表:
(单位:千元)的数据如下表:年份
2007
2008
2009
2010
2011
2012
2013
年份代号
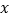
1
2
3
4
5
6
7
人均纯收入
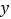
2.9
3.3
3.6
4.4
4.8
5.2
5.9
(1)求y关于
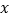 的线性回归方程;
的线性回归方程;(2)判断y与
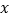 之间是正相关还是负相关?
之间是正相关还是负相关?(3)预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
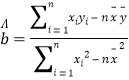 ,
,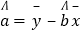
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
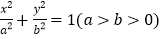 与
与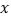 轴,
轴,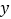 轴的正半轴分别交于A,B两点,原点O到直线AB的距离为
轴的正半轴分别交于A,B两点,原点O到直线AB的距离为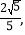 该椭圆的离心率为
该椭圆的离心率为
(1)求椭圆的方程
(2)是否存在过点P(
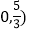 的直线
的直线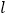 与椭圆交于M,N两个不同的点,使
与椭圆交于M,N两个不同的点,使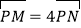 成立?若存在,求出
成立?若存在,求出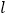 的方程;若不存在,说明理由。
的方程;若不存在,说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】据《中国新闻网》10月21日报道,全国很多省市将英语考试作为高考改革的重点,一时间“英语考试该如何改”引起广泛关注.为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3600人调查,就是否“取消英语听力”的问题,调查统计的结果如下表:
态度
调查人群应该取消
应该保留
无所谓
在校学生
2100人
120人
y人
社会人士
600人
x人
z人
已知在全体样本中随机抽取1人,抽到持“应该保留”态度的人的概率为0.05.
(Ⅰ)现用分层抽样的方法在所有参与调查的人中抽取360人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(Ⅱ)在持“应该保留”态度的人中,用分层抽样的方法抽取6人平均分成两组进行深入交流,求第一组中在校学生人数ξ的分布列和数学期望.
相关试题

