【题目】据《中国新闻网》10月21日报道,全国很多省市将英语考试作为高考改革的重点,一时间“英语考试该如何改”引起广泛关注.为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3600人调查,就是否“取消英语听力”的问题,调查统计的结果如下表:
态度 | 应该取消 | 应该保留 | 无所谓 |
在校学生 | 2100人 | 120人 | y人 |
社会人士 | 600人 | x人 | z人 |
已知在全体样本中随机抽取1人,抽到持“应该保留”态度的人的概率为0.05.
(Ⅰ)现用分层抽样的方法在所有参与调查的人中抽取360人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(Ⅱ)在持“应该保留”态度的人中,用分层抽样的方法抽取6人平均分成两组进行深入交流,求第一组中在校学生人数ξ的分布列和数学期望.
参考答案:
【答案】解:(I)∵抽到持“应该保留”态度的人的概率为0.05, ∴ ![]() =0.05,解得x=60.
=0.05,解得x=60.
∴持“无所谓”态度的人数共有3600﹣2100﹣120﹣600﹣60=720.
∴应在“无所谓”态度抽取720× ![]() =72人.
=72人.
(Ⅱ)由(I)知持“应该保留”态度的一共有180人,
∴在所抽取的6人中,在校学生为 ![]() =4人,社会人士为
=4人,社会人士为 ![]() =2人,
=2人,
于是第一组在校学生人数ξ=1,2,3,
P(ξ=1)= ![]() ,P(ξ=2)=
,P(ξ=2)= ![]() ,P(ξ=3)=
,P(ξ=3)= ![]() ,
,
即ξ的分布列为:
ξ | 1 | 2 | 3 |
P |
|
|
|
∴Eξ=1× ![]() +2×
+2× ![]() +3×
+3× ![]() =2
=2
【解析】(Ⅰ)先由抽到持“应该保留”态度的人的概率为0.05,由已知条件求出x,再求出持“无所谓”态度的人数,由此利用抽样比能求出应在“无所谓”态度抽取的人数.(Ⅱ)由题设知第一组在校学生人数ξ=1,2,3,分别求出P(ξ=1),P(ξ=2),P(ξ=3),由此能求出ξ的分布列和数学期望.
【考点精析】认真审题,首先需要了解分层抽样(先将总体中的所有单位按照某种特征或标志(性别、年龄等)划分成若干类型或层次,然后再在各个类型或层次中采用简单随机抽样或系用抽样的办法抽取一个子样本,最后,将这些子样本合起来构成总体的样本).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=cos2x+2sin2x+2sinx.
(Ⅰ)将函数f(2x)的图象向右平移 个单位得到函数g(x)的图象,若x∈[
个单位得到函数g(x)的图象,若x∈[ 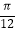 ,
, 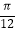 ],求函数g(x)的值域;
],求函数g(x)的值域;
(Ⅱ)已知a,b,c分别为△ABC中角A,B,C的对边,且满足f(A)=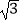 +1,A∈(0,
+1,A∈(0,  ),a=2
),a=2 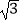 ,b=2,求△ABC的面积.
,b=2,求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某地区2007年至2013年农村居民家庭纯收入
 (单位:千元)的数据如下表:
(单位:千元)的数据如下表:年份
2007
2008
2009
2010
2011
2012
2013
年份代号
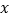
1
2
3
4
5
6
7
人均纯收入
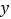
2.9
3.3
3.6
4.4
4.8
5.2
5.9
(1)求y关于
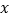 的线性回归方程;
的线性回归方程;(2)判断y与
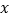 之间是正相关还是负相关?
之间是正相关还是负相关?(3)预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
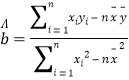 ,
,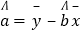
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
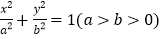 与
与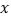 轴,
轴,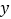 轴的正半轴分别交于A,B两点,原点O到直线AB的距离为
轴的正半轴分别交于A,B两点,原点O到直线AB的距离为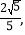 该椭圆的离心率为
该椭圆的离心率为
(1)求椭圆的方程
(2)是否存在过点P(
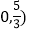 的直线
的直线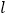 与椭圆交于M,N两个不同的点,使
与椭圆交于M,N两个不同的点,使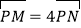 成立?若存在,求出
成立?若存在,求出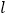 的方程;若不存在,说明理由。
的方程;若不存在,说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】正四面体ABCD中,M是棱AD的中点,O是点A在底面BCD内的射影,则异面直线BM与AO所成角的余弦值为____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四棱锥P﹣ABCD中,底面为矩形,PA⊥底面ABCD,PA=BC=1,AB=2,M为PC中点.
(Ⅰ)在图中作出平面ADM与PB的交点N,并指出点N所在位置(不要求给出理由);
(Ⅱ)在线段CD上是否存在一点E,使得直线AE与平面ADM所成角的正弦值为 ,若存在,请说明点E的位置;若不存在,请说明理由;
,若存在,请说明点E的位置;若不存在,请说明理由;
(Ⅲ)求二面角A﹣MD﹣C的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
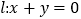 ,求:
,求:(1)点P(4,5)关于l的对称点;
(2)直线x-y-2=0关于直线l对称的直线方程.
相关试题

