【题目】已知函数f(x)=alnx+x2+bx(a为实常数).
(1)若a=﹣2,b=﹣3,求f(x)的单调区间;
(2)若b=0,且a>﹣2e2 , 求函数f(x)在[1,e]上的最小值及相应的x值;
(3)设b=0,若存在x∈[1,e],使得f(x)≤(a+2)x成立,求实数a的取值范围.
参考答案:
【答案】
(1)解:a=﹣2,b=﹣3时,f(x)=﹣2lnx+x2﹣3x,定义域为(0,+∞),
![]() ,
,
在(0,+∞)上,f′(2)=0,当x∈(0,2)时,f′(x)<0,当x∈(2,+∞)时,f′(x)>0,
所以函数f(x)的单调增区间为(2,+∞);单调减区间为(0,2);
(2)解:因为b=0,所以f(x)=alnx+x2 ![]() ,
,
x∈[1,e],2x2+a∈[a+2,a+2e2],
(i) 若a≥﹣2,f'(x)在[1,e]上非负(仅当a=﹣2,x=1时,f'(x)=0),
故函数f(x)在[1,e]上是增函数,
此时[f(x)]min=f(1)=1;
(ii)若﹣2e2<a<﹣2,a+2<0,a+2e2>0,
![]() ,x∈[1,e],
,x∈[1,e],
当 ![]() 时,f'(x)=0,
时,f'(x)=0, ![]() ,
,
当 ![]() 时,f'(x)<0,此时f(x)是减函数;
时,f'(x)<0,此时f(x)是减函数;
当 ![]() 时,f'(x)>0,此时f(x)是增函数.
时,f'(x)>0,此时f(x)是增函数.
故 ![]() ;
;
(3)解:b=0,f(x)=alnx+x2不等式f(x)≤(a+2)x,
即alnx+x2≤(a+2)x可化为a(x﹣lnx)≥x2﹣2x.
因为x∈[1,e],所以lnx≤1≤x且等号不能同时取,
所以lnx<x,即x﹣lnx>0,因而 ![]() (x∈[1,e]),
(x∈[1,e]),
令 ![]() (x∈[1,e]),又
(x∈[1,e]),又 ![]() ,
,
当x∈[1,e]时,x﹣1≥0,lnx≤1,x+2﹣2lnx>0,
从而g'(x)≥0(仅当x=1时取等号),所以g(x)在[1,e]上为增函数,
故g(x)的最小值为g(1)=﹣1,所以实数a的取值范围是[﹣1,+∞)
【解析】(1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;(2)求出函数的导数,通过讨论a的范围,求出函数的单调区间,从而求出函数的最小值即可;(3)问题转化为 ![]() (x∈[1,e]),令
(x∈[1,e]),令 ![]() (x∈[1,e]),根据函数的单调性求出a的范围即可.
(x∈[1,e]),根据函数的单调性求出a的范围即可.
【考点精析】掌握利用导数研究函数的单调性和函数的最大(小)值与导数是解答本题的根本,需要知道一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 圆心坐标为点
圆心坐标为点 为坐标原点,
为坐标原点, 轴、
轴、 轴被圆
轴被圆 截得的弦分别为
截得的弦分别为 、
、 .
.(1)证明:
 的面积为定值;
的面积为定值;(2)设直线
 与圆
与圆 交于
交于 两点,若
两点,若 ,求圆
,求圆 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 平面
平面 ,
, 为矩形,
为矩形, 分别为
分别为 的中点,
的中点, .
.
(1)求证:
 平面
平面 ;
;(2)求证:面
 平面
平面 ;
;(3)求点
 到平面
到平面 的距离.
的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A(x0 , 0),B(0,y0)两点分别在x轴和y轴上运动,且|AB|=1,若动点P(x,y)满足
 .
.
(1)求出动点P的轨迹对应曲线C的标准方程;
(2)一条纵截距为2的直线l1与曲线C交于P,Q两点,若以PQ直径的圆恰过原点,求出直线方程;
(3)直线l2:x=ty+1与曲线C交于A、B两点,E(1,0),试问:当t变化时,是否存在一直线l2 , 使△ABE的面积为 ?若存在,求出直线l2的方程;若不存在,说明理由.
?若存在,求出直线l2的方程;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为
 =0.85x-85.71,则下列结论中不正确的是
=0.85x-85.71,则下列结论中不正确的是A. y与x具有正的线性相关关系
B. 回归直线过样本点的中心(
 ,
, )
)C. 若该大学某女生身高增加1cm,则其体重约增加0.85kg
D. 若该大学某女生身高为170cm,则可断定其体重比为58.79kg
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学40名数学教师,按年龄从小到大编号为1,2,…40。现从中任意选取6人分成两组分配到A,B两所学校从事支教工作,其中三名编号较小的教师在一组,三名编号较大的教师在另一组,那么编号为8,12,28的数学教师同时入选并被分配到同一所学校的方法种数是
A. 220 B. 440 C. 255 D. 510
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义在
 上的函数
上的函数 ,如果满足:对任意
,如果满足:对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称函数
成立,则称函数 是
是 上的有界函数,其中
上的有界函数,其中 称为函数的上界.已知函数
称为函数的上界.已知函数 .
.(1)当
 时,求函数
时,求函数 在
在 上的值域,并判断函数
上的值域,并判断函数 在
在 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;(2)若函数
 在
在 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数 的取值范围;
的取值范围;(3)若
 ,函数
,函数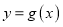 在
在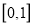 上的上界是
上的上界是 ,求
,求 的解析式.
的解析式.
相关试题

