搜索
【题目】已知圆
圆心坐标为点
为坐标原点，
轴、
轴被圆截得的弦分别为
、
.
（1）证明：
的面积为定值；
（2）设直线
与圆交于
两点，若
，求圆的方程.
参考答案：
【答案】（1）证明见解析；（2）
.
【解析】
（1）利用几何条件可知，
为直角三角形，且圆过原点，所以得知三角形两直角边边长，求得面积；
（2）由
及原点O在圆上，知OC
MN，所以
,求出
的值，再利用直线与圆的位置关系判断检验，符合题意的解，最后写出圆
的方程。
（1）因为
轴、
轴被圆截得的弦分别为
、
，
所以
经过，又为中点，所以
，所以
，所以的面积为定值.
（2）因为直线
与圆交于
两点，，
所以
的中垂线经过
，且过，所以
的方程
，
所以
，所以当
时，有圆心
，半径
，
所以圆心到直线的距离为
，
所以直线与圆交于点两点，故成立；
当
时，有圆心
，半径，所以圆心到直线的距离为
，所以直线与圆不相交，故（舍去），
综上所述，圆的方程为.
-
科目： 来源： 题型：
查看答案和解析>>【题目】设数列{an}的前n项和为
．
（1）求数列{an}的通项公式an；
（2）是否存在正整数n，使得
？若存在，求出n值；若不存在，说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系
中，曲线
的参数方程为
（
为参数），在以原点为极点， 
轴正半轴为极轴的极坐标系中，直线
的极坐标方程为
．（1）求曲线
的普通方程和直线
的倾斜角；（2）设点
，直线
和曲线
交于
两点，求
的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四棱锥
中，
平面
，
，
，
，点Q在棱AB上.（1）证明：
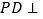平面
.（2）若三棱锥
的体积为
，求点B到平面PDQ的距离.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知
平面
，为矩形，
分别为
的中点，
.
（1）求证：
平面
；（2）求证：面
平面
；（3）求点
到平面
的距离. -
科目： 来源： 题型：
查看答案和解析>>【题目】已知A（x0 ， 0），B（0，y0）两点分别在x轴和y轴上运动，且|AB|=1，若动点P（x，y）满足
．
（1）求出动点P的轨迹对应曲线C的标准方程；
（2）一条纵截距为2的直线l1与曲线C交于P，Q两点，若以PQ直径的圆恰过原点，求出直线方程；
（3）直线l2：x=ty+1与曲线C交于A、B两点，E（1，0），试问：当t变化时，是否存在一直线l2 ， 使△ABE的面积为
？若存在，求出直线l2的方程；若不存在，说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）=alnx+x2+bx（a为实常数）．
（1）若a=﹣2，b=﹣3，求f（x）的单调区间；
（2）若b=0，且a＞﹣2e2 ， 求函数f（x）在[1，e]上的最小值及相应的x值；
（3）设b=0，若存在x∈[1，e]，使得f（x）≤（a+2）x成立，求实数a的取值范围．
相关试题
