【题目】已知A(x0 , 0),B(0,y0)两点分别在x轴和y轴上运动,且|AB|=1,若动点P(x,y)满足 ![]() .
.
(1)求出动点P的轨迹对应曲线C的标准方程;
(2)一条纵截距为2的直线l1与曲线C交于P,Q两点,若以PQ直径的圆恰过原点,求出直线方程;
(3)直线l2:x=ty+1与曲线C交于A、B两点,E(1,0),试问:当t变化时,是否存在一直线l2 , 使△ABE的面积为 ![]() ?若存在,求出直线l2的方程;若不存在,说明理由.
?若存在,求出直线l2的方程;若不存在,说明理由.
参考答案:
【答案】
(1)解:因为 ![]() ,
,
即 ![]() ,
,
所以 ![]() ,
,
所以 ![]()
又因为|AB|=1,所以 ![]() ,
,
即: ![]() ,
,
即 ![]() ,
,
所以椭圆的标准方程为 ![]() .
.
(2)解:直线l1斜率必存在,且纵截距为2,设直线为y=kx+2联立直线l1和椭圆方程 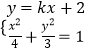 ,
,
得:(3+4k2)x2+16kx+4=0,
由△>0,得 ![]() (*),
(*),
设P(x1,y1),Q(x2,y2),
则 ![]() (1)
(1)
以PQ直径的圆恰过原点,
所以OP⊥OQ, ![]() ,
,
即x1x2+y1y2=0,
也即x1x2+(kx1+2)(kx2+2)=0,
即(1+k2)x1x2+2k(x1+x2)+4=0,
将(1)式代入,得 ![]() ﹣
﹣ ![]() +4=0,
+4=0,
即4(1+k2)﹣32k2+4(3+4k2)=0,
解得 ![]() ,满足(*)式,
,满足(*)式,
所以 ![]() .
.
所以直线方程为y=± ![]() x+2
x+2
(3)解:由方程组 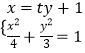 ,得(3t2+4)y2+6ty﹣9=0(*)
,得(3t2+4)y2+6ty﹣9=0(*)
设A(x1,y1),B(x2,y2),
则 ![]()
所以 ![]() ,
,
因为直线l:x=ty+1过点F(1,0),
所以S△ABE= ![]() |EF||y1﹣y2|=
|EF||y1﹣y2|= ![]() ×2×
×2× ![]() =
= ![]()
令= ![]() =2
=2 ![]() ,则
,则 ![]() 不成立
不成立
故不存在直线l满足题意
【解析】(1)根据向量的坐标运算,以及|AB|=1,得到椭圆的标准方程为 ![]() .(2)直线l1斜率必存在,且纵截距为2,根据直线与椭圆的位置关系,即可求出k的值,问题得以解决.(3)根据直线和椭圆额位置关系,以及三角形的面积公式得到S△ABE=
.(2)直线l1斜率必存在,且纵截距为2,根据直线与椭圆的位置关系,即可求出k的值,问题得以解决.(3)根据直线和椭圆额位置关系,以及三角形的面积公式得到S△ABE= ![]() ,令=
,令= ![]() =2
=2 ![]() ,则
,则 ![]() 不成立,问题得以解决.
不成立,问题得以解决.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,
中, 平面
平面 ,
, ,
,
 ,
, ,点Q在棱AB上.
,点Q在棱AB上.(1)证明:
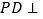 平面
平面 .
.(2)若三棱锥
 的体积为
的体积为 ,求点B到平面PDQ的距离.
,求点B到平面PDQ的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 圆心坐标为点
圆心坐标为点 为坐标原点,
为坐标原点, 轴、
轴、 轴被圆
轴被圆 截得的弦分别为
截得的弦分别为 、
、 .
.(1)证明:
 的面积为定值;
的面积为定值;(2)设直线
 与圆
与圆 交于
交于 两点,若
两点,若 ,求圆
,求圆 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 平面
平面 ,
, 为矩形,
为矩形, 分别为
分别为 的中点,
的中点, .
.
(1)求证:
 平面
平面 ;
;(2)求证:面
 平面
平面 ;
;(3)求点
 到平面
到平面 的距离.
的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=alnx+x2+bx(a为实常数).
(1)若a=﹣2,b=﹣3,求f(x)的单调区间;
(2)若b=0,且a>﹣2e2 , 求函数f(x)在[1,e]上的最小值及相应的x值;
(3)设b=0,若存在x∈[1,e],使得f(x)≤(a+2)x成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为
 =0.85x-85.71,则下列结论中不正确的是
=0.85x-85.71,则下列结论中不正确的是A. y与x具有正的线性相关关系
B. 回归直线过样本点的中心(
 ,
, )
)C. 若该大学某女生身高增加1cm,则其体重约增加0.85kg
D. 若该大学某女生身高为170cm,则可断定其体重比为58.79kg
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学40名数学教师,按年龄从小到大编号为1,2,…40。现从中任意选取6人分成两组分配到A,B两所学校从事支教工作,其中三名编号较小的教师在一组,三名编号较大的教师在另一组,那么编号为8,12,28的数学教师同时入选并被分配到同一所学校的方法种数是
A. 220 B. 440 C. 255 D. 510
相关试题

