【题目】对于![]() 维向量
维向量![]() ,若对任意
,若对任意![]() 均有
均有![]() 或
或![]() ,则称
,则称![]() 为
为![]() 维
维![]() 向量. 对于两个
向量. 对于两个![]() 维
维![]() 向量
向量![]() 定义
定义![]() .
.
(1)若![]() , 求
, 求![]() 的值;
的值;
(2)现有一个![]() 维
维![]() 向量序列:
向量序列: ![]() 若
若![]() 且满足:
且满足: ![]() ,求证:该序列中不存在
,求证:该序列中不存在![]() 维
维![]() 向量
向量![]() .
.
(3) 现有一个![]() 维
维![]() 向量序列:
向量序列: ![]() 若
若![]() 且满足:
且满足: ![]() ,若存在正整数
,若存在正整数![]() 使得
使得![]() 为
为![]() 维
维![]() 向量序列中的项,求出所有的
向量序列中的项,求出所有的![]() .
.
参考答案:
【答案】(1)![]() (2)不存在(3)
(2)不存在(3)![]()
【解析】试题分析:(Ⅰ)根据![]() 的定义可求得其值;(Ⅱ)利用反证法,向量
的定义可求得其值;(Ⅱ)利用反证法,向量![]() 的每一个分量变为
的每一个分量变为![]() ,都需要奇数次变化,根据
,都需要奇数次变化,根据![]() ,得出矛盾;(Ⅲ)根据题意可得
,得出矛盾;(Ⅲ)根据题意可得![]() .
.
试题解析:(Ⅰ)由于![]() ,
, ![]() ,由定义
,由定义![]() ,
,
可得![]() .
.
(Ⅱ)反证法:若结论不成立,即存在一个含![]() 维
维![]() 向量序列
向量序列![]() ,
,
使得![]() ,
, ![]() .
.
因为向量![]() 的每一个分量变为
的每一个分量变为![]() ,都需要奇数次变化,
,都需要奇数次变化,
不妨设![]() 的第
的第![]() 个分量
个分量![]() 变化了
变化了![]() 次之后变成
次之后变成![]() ,
,
所以将![]() 中所有分量
中所有分量![]() 变为
变为![]() 共需要
共需要![]()
![]() 次,此数为奇数.
次,此数为奇数.
又因为![]() ,说明
,说明![]() 中的分量有
中的分量有![]() 个数值发生改变,
个数值发生改变,
进而变化到![]() ,所以共需要改变数值
,所以共需要改变数值![]() 次,此数为偶数,所以矛盾.
次,此数为偶数,所以矛盾.
所以该序列中不存在![]() 维
维![]() 向量
向量![]() .
.
(Ⅲ)此时![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某地高一学生的体能状况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形的面积之比为2:4:17:15:9:3,第二小组频数为12.
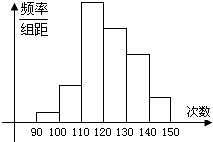
(1)第二小组的频率是多少?样本容量是多少?
(2)若次数在110以上为达标,试估计全体高一学生的达标率为多少?
(3)通过该统计图,可以估计该地学生跳绳次数的众数是 , 中位数是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校一个生物兴趣小组对学校的人工湖中养殖的某种鱼类进行观测研究,在饲料充足的前提下,兴趣小组对饲养时间x(单位:月)与这种鱼类的平均体重y(单位:千克)得到一组观测值,如下表:
xi(月)
1
2
3
4
5
yi(千克)
0.5
0.9
1.7
2.1
2.8
(参考公式:
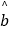 =
= 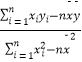 ,
, 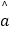 =
= 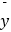 ﹣
﹣ 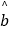
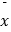 )
)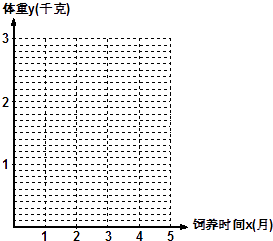
(1)在给出的坐标系中,画出关于x,y两个相关变量的散点图.
(2)请根据上表提供的数据,用最小二乘法求出变量y关于变量x的线性回归直线方程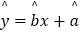 .
.
(3)预测饲养满12个月时,这种鱼的平均体重(单位:千克) -
科目: 来源: 题型:
查看答案和解析>>【题目】在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个球被取出的可能性相等.
(1)求取出的两个球上标号为相同数字的概率;
(2)求取出的两个球上标号之积能被3整除的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】若点(p,q),在|p|≤3,|q|≤3中按均匀分布出现.
(1)点M(x,y)横、纵坐标分别由掷骰子确定,第一次确定横坐标,第二次确定纵坐标,则点M(x,y)落在上述区域的概率?
(2)试求方程x2+2px﹣q2+1=0有两个实数根的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知动点M(x,y)到直线l:x=4的距离是它到点N(1,0)的距离的2倍.
(1)求动点M的轨迹C的方程;
(2)过点P(0,3)的直线m与轨迹C交于A,B两点,若A是PB的中点,求直线m的斜率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设{an}是由正数组成的等比数列,公比q=2,且a1a2a3…a30=230 , 那么a3a6a9…a30等于( )
A.210
B.220
C.216
D.215
相关试题

