【题目】某学校一个生物兴趣小组对学校的人工湖中养殖的某种鱼类进行观测研究,在饲料充足的前提下,兴趣小组对饲养时间x(单位:月)与这种鱼类的平均体重y(单位:千克)得到一组观测值,如下表:
xi(月) | 1 | 2 | 3 | 4 | 5 |
yi(千克) | 0.5 | 0.9 | 1.7 | 2.1 | 2.8 |
(参考公式: ![]() =
= 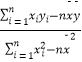 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
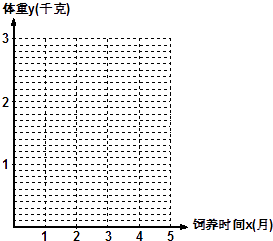
![]() )
)
(1)在给出的坐标系中,画出关于x,y两个相关变量的散点图.
(2)请根据上表提供的数据,用最小二乘法求出变量y关于变量x的线性回归直线方程 ![]() .
.
(3)预测饲养满12个月时,这种鱼的平均体重(单位:千克)
参考答案:
【答案】
(1)解:散点图如图所示

(2)解:由题设 ![]() =3,
=3, ![]() =1.6,
=1.6,
∴ ![]() =
= 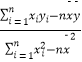 =
= ![]() =0.58,
=0.58,
a= ![]() ﹣
﹣ ![]()
![]() =﹣0.14
=﹣0.14
故回归直线方程为y=0.58x﹣0.14
(3)解:当x=12时,y=0.58×12﹣0.14=6.82
饲养满12个月时,这种鱼的平均体重约为6.82千克
【解析】(1)利用所给数据,可得散点图;(2)利用公式,计算回归系数,即可得到回归方程;(3)x=12代入回归方程,即可得到结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明计划在8月11日至8月20日期间游览某主题公园.根据旅游局统计数据,该主题公园在此期间“游览舒适度”(即在园人数与景区主管部门核定的最大瞬时容量之比,40%以下为舒适,40%—60%为一般,60%以上为拥挤)情况如图所示.小明随机选择8月11日至8月19日中的某一天到达该主题公园,并游览2天.
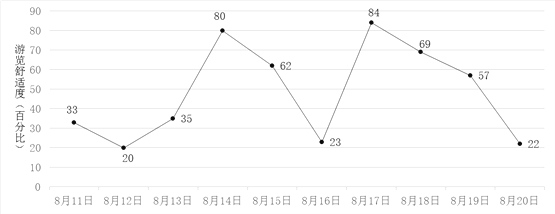 (Ⅰ)求小明连续两天都遇上拥挤的概率;
(Ⅰ)求小明连续两天都遇上拥挤的概率;(Ⅱ)设
 是小明游览期间遇上舒适的天数,求
是小明游览期间遇上舒适的天数,求 的分布列和数学期望;
的分布列和数学期望;(Ⅲ)由图判断从哪天开始连续三天游览舒适度的方差最大?(结论不要求证明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】从甲、乙两名学生中选拔一人参加射箭比赛,为此需要对他们的射箭水平进行测试.现这两名学生在相同条件下各射箭10次,命中的环数如表:
甲
8
9
7
9
7
6
10
10
8
6
乙
10
9
8
6
8
7
9
7
8
8
(1)计算甲、乙两人射箭命中环数的平均数和标准差;
(2)比较两个人的成绩,然后决定选择哪名学生参加射箭比赛. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某地高一学生的体能状况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形的面积之比为2:4:17:15:9:3,第二小组频数为12.
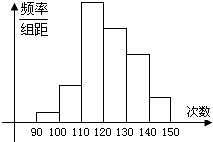
(1)第二小组的频率是多少?样本容量是多少?
(2)若次数在110以上为达标,试估计全体高一学生的达标率为多少?
(3)通过该统计图,可以估计该地学生跳绳次数的众数是 , 中位数是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个球被取出的可能性相等.
(1)求取出的两个球上标号为相同数字的概率;
(2)求取出的两个球上标号之积能被3整除的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于
 维向量
维向量 ,若对任意
,若对任意 均有
均有 或
或 ,则称
,则称 为
为 维
维 向量. 对于两个
向量. 对于两个 维
维 向量
向量 定义
定义 .
.(1)若
 , 求
, 求 的值;
的值;(2)现有一个
 维
维 向量序列:
向量序列:  若
若 且满足:
且满足:  ,求证:该序列中不存在
,求证:该序列中不存在 维
维 向量
向量 .
.(3) 现有一个
 维
维 向量序列:
向量序列:  若
若 且满足:
且满足:  ,若存在正整数
,若存在正整数 使得
使得 为
为 维
维 向量序列中的项,求出所有的
向量序列中的项,求出所有的 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】若点(p,q),在|p|≤3,|q|≤3中按均匀分布出现.
(1)点M(x,y)横、纵坐标分别由掷骰子确定,第一次确定横坐标,第二次确定纵坐标,则点M(x,y)落在上述区域的概率?
(2)试求方程x2+2px﹣q2+1=0有两个实数根的概率.
相关试题

