【题目】已知函数f(x)= ![]() 的定义域为集合A,B={x∈Z|2<x<10},C={x∈R|x<a或x>a+1}
的定义域为集合A,B={x∈Z|2<x<10},C={x∈R|x<a或x>a+1}
(1)求A,(RA)∩B;
(2)若A∪C=R,求实数a的取值范围.
参考答案:
【答案】
(1)解:由题意 ![]() ,解得7>x≥3,故A={x∈R|3≤x<7},
,解得7>x≥3,故A={x∈R|3≤x<7},
B={x∈Z|2<x<10}═{x∈Z|3,4,5,6,7,8,9},
∴(CRA)∩B{7,8,9}
(2)解:∵A∪C=R,C={x∈R|x<a或x>a+1}
∴ ![]() 解得3≤a<6
解得3≤a<6
实数a的取值范围是3≤a<6
【解析】(1)先求出集合A,化简集合B,根据 根据集合的运算求,(CRA)∩B;(2)若A∪C=R,则可以比较两个集合的端点,得出参数所满足的不等式解出参数的取值范围.
【考点精析】利用交、并、补集的混合运算和函数的定义域及其求法对题目进行判断即可得到答案,需要熟知求集合的并、交、补是集合间的基本运算,运算结果仍然还是集合,区分交集与并集的关键是“且”与“或”,在处理有关交集与并集的问题时,常常从这两个字眼出发去揭示、挖掘题设条件,结合Venn图或数轴进而用集合语言表达,增强数形结合的思想方法;求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四棱锥
 的底面为平行四边形,且
的底面为平行四边形,且 ,
, ,
, 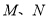 分别为
分别为 中点,过
中点,过 作平面
作平面 分别与线段
分别与线段 相交于点
相交于点 .
.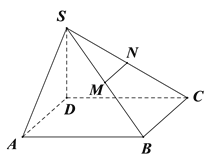
(Ⅰ)在图中作出平面
 使面
使面 ‖
‖ (不要求证明);
(不要求证明);(II)若
 ,在(Ⅰ)的条件下求多面体
,在(Ⅰ)的条件下求多面体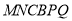 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 的顶点
的顶点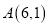 ,
, 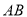 边上的中线
边上的中线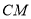 所在直线方程为
所在直线方程为 ,
, 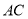 边上的高
边上的高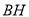 所在直线方程为
所在直线方程为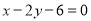 .
. (1)求点
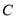 的坐标;
的坐标;(2)求直线
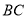 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义函数y=f(x),x∈D(定义域),若存在常数C,对于任意x1∈D,存在唯一的x2∈D,使得
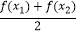 =C,则称函数f(x)在D上的“均值”为C,已知f(x)=lgx,x∈[10,100],则函数f(x)在[10,100]上的均值为( )
=C,则称函数f(x)在D上的“均值”为C,已知f(x)=lgx,x∈[10,100],则函数f(x)在[10,100]上的均值为( )
A.
B.
C.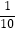
D.10 -
科目: 来源: 题型:
查看答案和解析>>【题目】为了调查中小学课外使用互联网的情况,教育部向华东、华北、华南和西部地区60所中小学发出问卷
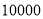 份,
份,  名学生参加了问卷调查,并根据所得数据画出样本的频率分布直方图(如图).
名学生参加了问卷调查,并根据所得数据画出样本的频率分布直方图(如图).(1)要从这
 名中小学中用分层抽样的方法抽取
名中小学中用分层抽样的方法抽取 名中小学生进一步调查,则在
名中小学生进一步调查,则在 (小时)时间段内应抽出的人数是多少?
(小时)时间段内应抽出的人数是多少?(2)若希望
 的中小学生每天使用互联网时间不少于
的中小学生每天使用互联网时间不少于 (小时),请估计
(小时),请估计 的值,并说明理由.
的值,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 且
且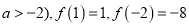 ,且,函数
,且,函数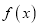 的图象与直线
的图象与直线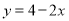 相切.
相切.(1)求
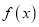 的解析式;
的解析式;(2)若当
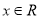 时,
时, 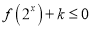 恒成立,求实数
恒成立,求实数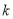 的取值范围;
的取值范围;(3)是否存在区间
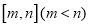 ,使得
,使得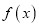 在区间
在区间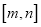 上的值域恰好为
上的值域恰好为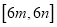 ?若存在,请求出区间
?若存在,请求出区间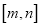 ,若不存在,请说明理由.
,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
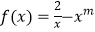 ,且
,且 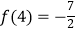 .
.
(1)求m的值;
(2)判断f(x)在(0,+∞)上的单调性,并给予证明;
(3)求函数f(x)在区间[﹣5,﹣1]上的最值.
相关试题

