【题目】已知![]() 的顶点
的顶点![]() ,
, ![]() 边上的中线
边上的中线![]() 所在直线方程为
所在直线方程为![]() ,
, ![]() 边上的高
边上的高![]() 所在直线方程为
所在直线方程为![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)求直线![]() 的方程.
的方程.
参考答案:
【答案】(1) C(5,3);(2) 6x-5y-15=0.
【解析】试题分析:(1)已知![]() 边上的高
边上的高![]() 所在直线方程,可得
所在直线方程,可得![]() 所在直线的斜率,联立
所在直线的斜率,联立![]() 和
和![]() 的直线方程即可求出点
的直线方程即可求出点![]() 的坐标(2)
的坐标(2)![]() 所在直线方程是
所在直线方程是![]() 边上的中线所在直线方程,则
边上的中线所在直线方程,则![]() 的中点坐标满足此直线方程,代入直线方程求得B 点所在直线方程联立直线方程求出B(0,-3),即可求出直线
的中点坐标满足此直线方程,代入直线方程求得B 点所在直线方程联立直线方程求出B(0,-3),即可求出直线![]() 的方程
的方程
解析:(1)依题意知:kAC=-2,A(6,1),
∴lAC为2x+y-13=0,
联立lAC、lCM得![]() ∴C(5,3).
∴C(5,3).
(2)设B(x0,y0),AB的中点M为(![]() ,
,![]() ),
),
代入2x-y-7=0,得2x0-y0-3=0,
∴![]() ∴B(0,-3),
∴B(0,-3),
∴kBC=![]() ,∴直线BC的方程为y=
,∴直线BC的方程为y=![]() x-3,
x-3,
即6x-5y-15=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知实数a≠0,函数f(x)=
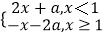 ,若f(1﹣a)=f(1+a),则a的值为( )
,若f(1﹣a)=f(1+a),则a的值为( )
A.﹣
B.﹣
C.﹣ 或﹣
或﹣ 
D.﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系中,以原点为极点,
 轴正半轴为极轴建立坐标系,直线
轴正半轴为极轴建立坐标系,直线 的极坐标方程为
的极坐标方程为 ,曲线
,曲线 的参数方程为
的参数方程为 ,(
,(  为参数).
为参数).(Ⅰ)求直线
 的直角坐标方程和曲线
的直角坐标方程和曲线 的普通方程;
的普通方程;(Ⅱ)曲线
 交
交 轴于
轴于 两点,且点
两点,且点 ,
,  为直线
为直线 上的动点,求
上的动点,求 周长的最小值.
周长的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知四棱锥
 的底面为平行四边形,且
的底面为平行四边形,且 ,
, ,
, 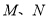 分别为
分别为 中点,过
中点,过 作平面
作平面 分别与线段
分别与线段 相交于点
相交于点 .
.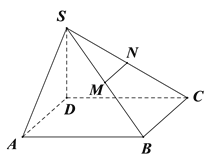
(Ⅰ)在图中作出平面
 使面
使面 ‖
‖ (不要求证明);
(不要求证明);(II)若
 ,在(Ⅰ)的条件下求多面体
,在(Ⅰ)的条件下求多面体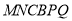 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义函数y=f(x),x∈D(定义域),若存在常数C,对于任意x1∈D,存在唯一的x2∈D,使得
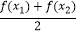 =C,则称函数f(x)在D上的“均值”为C,已知f(x)=lgx,x∈[10,100],则函数f(x)在[10,100]上的均值为( )
=C,则称函数f(x)在D上的“均值”为C,已知f(x)=lgx,x∈[10,100],则函数f(x)在[10,100]上的均值为( )
A.
B.
C.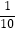
D.10 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
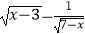 的定义域为集合A,B={x∈Z|2<x<10},C={x∈R|x<a或x>a+1}
的定义域为集合A,B={x∈Z|2<x<10},C={x∈R|x<a或x>a+1}
(1)求A,(RA)∩B;
(2)若A∪C=R,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了调查中小学课外使用互联网的情况,教育部向华东、华北、华南和西部地区60所中小学发出问卷
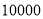 份,
份,  名学生参加了问卷调查,并根据所得数据画出样本的频率分布直方图(如图).
名学生参加了问卷调查,并根据所得数据画出样本的频率分布直方图(如图).(1)要从这
 名中小学中用分层抽样的方法抽取
名中小学中用分层抽样的方法抽取 名中小学生进一步调查,则在
名中小学生进一步调查,则在 (小时)时间段内应抽出的人数是多少?
(小时)时间段内应抽出的人数是多少?(2)若希望
 的中小学生每天使用互联网时间不少于
的中小学生每天使用互联网时间不少于 (小时),请估计
(小时),请估计 的值,并说明理由.
的值,并说明理由.
相关试题

