【题目】医院到某社区检查老年人的体质健康情况,从该社区全体老人中,随机抽取12名进行体质健康测试,测试成绩(百分制)如下:65,78,90,86,52,87,72,86,87,98,88,86.根据老年人体质健康标准,成绩不低于80的为优良.
(1)将频率视为概率,根据样本估计总体的思想,在该社区全体老年人中任选3人进行体质健康测试,求至少有1人成绩是“优良”的概率;
(2)从抽取的12人中随机选取3人,记ξ表示成绩“优良”的人数,求ξ的分布列和期望.
参考答案:
【答案】
(1)解:抽取的12人中成绩是“优良”的频率为 ![]() ,
,
故从该社区中任选1人,成绩是“优良”的概率为 ![]() ,
,
设“在该社区老人中任选三人,至少有1人成绩是‘优良’的事件”为A,
则P(A)=1﹣ ![]() =
= ![]() .
.
(2)解:由题意得ξ的可能取值为0,1,2,3,
P(ξ=0)= ![]() =
= ![]() ,
,
P(ξ=1)= ![]() =
= ![]() ,
,
P(ξ=2)= ![]() =
= ![]() ,
,
P(ξ=3)= ![]() =
= ![]() ,
,
∴ξ的分布列为:
ξ | 0 | 1 | 2 | 3 |
P |
|
|
|
|
Eξ= ![]() =2
=2
【解析】(1)从该社区中任选1人,成绩是“优良”的概率为 ![]() ,由此能求出在该社区老人中任选三人,至少有1人成绩是‘优良’的概率.(2)由题意得ξ的可能取值为0,1,2,3,分别求出相应的概率,由此能求出ξ的分布列和期望.
,由此能求出在该社区老人中任选三人,至少有1人成绩是‘优良’的概率.(2)由题意得ξ的可能取值为0,1,2,3,分别求出相应的概率,由此能求出ξ的分布列和期望.
【考点精析】利用离散型随机变量及其分布列对题目进行判断即可得到答案,需要熟知在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知映射f:A→B,其中A=B=R,对应法则f:x→y=(
 )
) 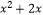 ,若对实数m∈B,在集合A中存在元素与之对应,则m的取值范围是( )
,若对实数m∈B,在集合A中存在元素与之对应,则m的取值范围是( )
A.(﹣∞,2]
B.[2,+∞)
C.(2,+∞)
D.(0,2] -
科目: 来源: 题型:
查看答案和解析>>【题目】已知(x+
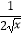 )n的展开式中的第二项和第三项的系数相等.
)n的展开式中的第二项和第三项的系数相等.
(1)求n的值;
(2)求展开式中所有二项式系数的和;
(3)求展开式中所有的有理项. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两名同学参加定点投篮测试,已知两人投中的概率分别是
 和
和 ,假设两人投篮结果相互没有影响,每人各次投球是否投中也没有影响.
,假设两人投篮结果相互没有影响,每人各次投球是否投中也没有影响.(Ⅰ)若每人投球3次(必须投完),投中2次或2次以上,记为达标,求甲达标的概率;
(Ⅱ)若每人有4次投球机会,如果连续两次投中,则记为达标.达标或能断定不达标,则终止投篮.记乙本次测试投球的次数为
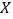 ,求
,求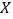 的分布列和数学期望
的分布列和数学期望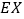 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 的参数方程为
的参数方程为 (
( 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,  轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆 的极坐标方程为
的极坐标方程为 ,直线
,直线 与圆
与圆 交于
交于 ,
,  两点.
两点.(1)求圆
 的直角坐标方程及弦
的直角坐标方程及弦 的长;
的长;(2)动点
 在圆
在圆 上(不与
上(不与 ,
,  重合),试求
重合),试求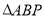 的面积的最大值.
的面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
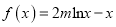 ,
, 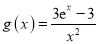 (
(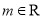 ,
, 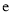 为自然对数的底数).
为自然对数的底数).(1)试讨论函数
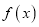 的极值情况;
的极值情况;(2)证明:当
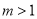 且
且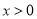 时,总有
时,总有 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在各棱长均为2的三棱柱ABC﹣A1B1C1中,侧面A1ACC1⊥底面ABC,且∠A1AC=
 ,点O为AC的中点.
,点O为AC的中点. 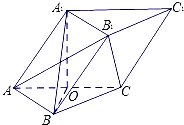
(1)求证:AC⊥平面A1OB;
(2)求二面角B1﹣AC﹣B的余弦值.
相关试题

