【题目】已知直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与圆
与圆![]() 交于
交于![]() ,
, ![]() 两点.
两点.
(1)求圆![]() 的直角坐标方程及弦
的直角坐标方程及弦![]() 的长;
的长;
(2)动点![]() 在圆
在圆![]() 上(不与
上(不与![]() ,
, ![]() 重合),试求
重合),试求![]() 的面积的最大值.
的面积的最大值.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)利用平面直角坐标系与极坐标系间的转化关系,可得圆的直角坐标方程,将直线的参数方程代入,利用参数的几何意义可求得弦![]() 的长;(2)写出圆的参数方程,利用点到直线的距离公式,可得
的长;(2)写出圆的参数方程,利用点到直线的距离公式,可得![]() ,可求出
,可求出![]() 的最大值,即求得
的最大值,即求得![]() 的面积的最大值.
的面积的最大值.
试题分析:(1)由![]() 得
得![]() ,所以
,所以![]() ,所以圆
,所以圆![]() 的直角坐标方程为
的直角坐标方程为![]() .将直线
.将直线![]() 的参数方程代入圆
的参数方程代入圆![]()
![]() ,并整理得
,并整理得![]() ,解得
,解得![]() ,
, ![]() .所以直线
.所以直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() .
.
(2)直线![]() 的普通方程为
的普通方程为![]() .圆
.圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),
为参数),
可设曲线![]() 上的动点
上的动点![]() ,则点
,则点![]() 到直线
到直线![]() 的距离
的距离![]()
![]() ,当
,当![]() 时,
时, ![]() 取最大值,且
取最大值,且![]() 的最大值为
的最大值为![]() .
.
所以![]() ,即
,即![]() 的面积的最大值为
的面积的最大值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知球内接四棱锥
 的高为
的高为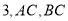 相交于
相交于 ,球的表面积为
,球的表面积为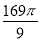 ,若
,若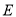 为
为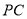 中点.
中点.(1)求证:
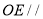 平面
平面 ;
;(2)求二面角
 的余弦值.
的余弦值.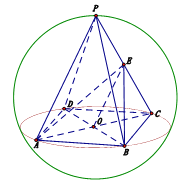
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD 中,AD⊥平面ABE,AE=FB=BC=2,F为CE上的点,且BF⊥平面ACE,AC,BD交于G点
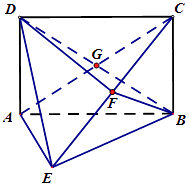
(1)求证:AE∥平面BFD
(2)求证:AE⊥平面BCE
(3)求三棱柱C﹣BGF的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)讨论函数
 的单调性;
的单调性;(2)当
 时,若函数
时,若函数 的导函数
的导函数 的图象与
的图象与 轴交于
轴交于 ,
,  两点,其横坐标分别为
两点,其横坐标分别为 ,
,  ,线段
,线段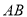 的中点的横坐标为
的中点的横坐标为 ,且
,且 ,
,  恰为函数
恰为函数 的零点,求证:
的零点,求证:  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的不等式ax2﹣(a+2)x+2<0.
(1)当a=﹣1时,解不等式;
(2)当a∈R时,解不等式. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数:f(x)=x2+bx+c,其中:0≤b≤4,0≤c≤4,记函数f(x)满足条件:
 的事件为A,则事件A发生的概率为( )
的事件为A,则事件A发生的概率为( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若直线ax﹣by+2=0(a>0,b>0)被圆x2+y2+4x﹣4y﹣1=0所截得的弦长为6,则
 的最小值为( )
的最小值为( )
A.10
B.
C.
D.
相关试题

