【题目】对于定义域为R的函数f(x),若满足①f(0)=0;②当x∈R,且x≠0时,都有xf'(x)>0;③当x1≠x2 , 且f(x1)=f(x2)时,x1+x2<0,则称f(x)为“偏对称函数”. 现给出四个函数:g(x)=  ;φ(x)=ex﹣x﹣1.
;φ(x)=ex﹣x﹣1.
则其中是“偏对称函数”的函数个数为 .
参考答案:
【答案】2
【解析】经验证,g(x),h(x),Φ(x),φ(x)都满足条件①; xf′(x)>0 ![]() ,或
,或 ![]() .即条件②等价于函数f(x)在区间(﹣∞,0)上单调递减,在区间(0,+∞)上单调递增.
.即条件②等价于函数f(x)在区间(﹣∞,0)上单调递减,在区间(0,+∞)上单调递增.
而容易验证g(x)是奇函数,由及函数的性质可知g(x)在区间(﹣∞,0)和(0,+∞)上单调性相同,故g(x)不满足条件②.
由复合函数的单调性法则知h(x)在区间(﹣∞,0)上单调递减,显然在(0,+∞)上单调递增,故h(x)满足条件②.
Φ′(x)=﹣3x2+3x,xΦ′(x)=﹣3x3+3x2=﹣3x2(x﹣1),当x>1时,xΦ′(x)<0,故Φ(x)不满足条件②.
φ′(x)=ex﹣1,xφ′(x)=x(ex﹣1),满足条件②.
故由条件②可排除g(x)和Φ(x);
由函数h(x)的单调性知:当x1≠x2 , 且h(x1)=h(x2)时,x1x2<0,不妨设x1<0<x2 .
则ln(﹣x1+1)=2x2 , 设F(x)=ln(x+1)﹣2x,x>0.则F′(x)= ![]() <0,F(x)在(0,+∞)上是减函数,
<0,F(x)在(0,+∞)上是减函数,
所以F(x2)<F(0)=0,即ln(x2+1)<2x2 , 即ln(x2+1)<ln(﹣x1+1),所以x2+1<﹣x1+1,即x1+x2<0,故h(x)也满足条件③,所以h(x)是“偏对称函数”.
由φ(x)的单调性知当x1≠x2 , 且φ(x1)=φ(x2)时,x1x2<0,不妨设x1<0<x2 .
则 ![]() ,﹣x2<0,φ(x1)﹣φ(﹣x2)=φ(x2)﹣φ(﹣x2)=
,﹣x2<0,φ(x1)﹣φ(﹣x2)=φ(x2)﹣φ(﹣x2)= ![]() .
.
令F(x)=ex﹣e﹣x﹣2x,F′(x)= ![]() ,当且仅当ex=e﹣x即x=0时,“=”成立,
,当且仅当ex=e﹣x即x=0时,“=”成立,
所以F(x)在[0,+∞)上是增函数,所以F(x2)>F(0)=0,即φ(x1)﹣φ(﹣x2)>0,所以φ(x1)>φ(﹣x2),所以x1<﹣x2 , 所以x1+x2<0.所以φ(x)是“偏对称函数”.
所以答案是:2
【考点精析】根据题目的已知条件,利用函数的值和利用导数研究函数的单调性的相关知识可以得到问题的答案,需要掌握函数值的求法:①配方法(二次或四次);②“判别式法”;③反函数法;④换元法;⑤不等式法;⑥函数的单调性法;一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
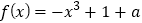 (
( 是自然对数的底数)与
是自然对数的底数)与 的图象上存在关于
的图象上存在关于 轴对称的点,则实数
轴对称的点,则实数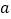 的取值范围是( )
的取值范围是( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱
 中,
中,  .
.(Ⅰ)证明:
 ;
;(Ⅱ)平面

 平面
平面 ,
,  ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三点
 ,
, ,
, ,曲线
,曲线 上任意一点
上任意一点 满足
满足 .
.(1)求
 的方程;
的方程;(2)动点

 在曲线
在曲线 上,
上, 是曲线
是曲线 在
在 处的切线.问:是否存在定点
处的切线.问:是否存在定点 使得
使得 与
与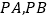 都相交,交点分别为
都相交,交点分别为 ,且
,且 与
与 的面积之比为常数?若存在,求
的面积之比为常数?若存在,求 的值;若不存在,说明理由.
的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)求函数
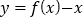 的单调区间;
的单调区间;(2)求证:函数
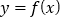 和
和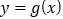 在公共定义域内,
在公共定义域内,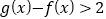 恒成立;
恒成立;(3)若存在两个不同的实数
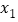 ,
,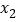 ,满足
,满足 ,求证:
,求证: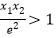 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且B=60°,c=4.
(Ⅰ)若b=6,求角C的正弦值及△ABC的面积;
(Ⅱ)若D,E在线段BC上,且BD=DE=EC, ,求AD的长.
,求AD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,侧面PAD⊥底面ABCD,底面ABCD是平行四边形,∠ABC=45°,AD=AP=2,
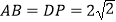 ,E为CD的中点,点F在线段PB上.
,E为CD的中点,点F在线段PB上. 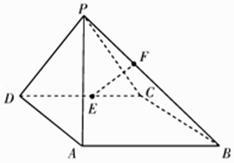
(Ⅰ)求证:AD⊥PC;
(Ⅱ)试确定点F的位置,使得直线EF与平面PDC所成的角和直线EF与平面ABCD所成的角相等.
相关试题

