【题目】如图,三棱柱![]() 中,
中, ![]() .
.
(Ⅰ)证明: ![]() ;
;
(Ⅱ)平面![]()
![]() 平面
平面![]() ,
, ![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.

参考答案:
【答案】(1)证明见解析;(2) ![]() .
.
【解析】试题分析:
(1)利用题意首先证得![]() ,然后利用线面垂直的定义即可证得题中的结论;
,然后利用线面垂直的定义即可证得题中的结论;
(2)建立空间直角坐标系,结合平面的法向量和直线的方向向量可得直线![]() 与平面
与平面![]() 所成角的正弦值是
所成角的正弦值是![]() .
.
试题解析:
(1)证明:如图所示,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
, ![]() ,
, ![]() .因为
.因为![]() ,
,
所以![]() .由于
.由于![]() ,
, ![]() ,
,
故![]() 为等边三角形,所以
为等边三角形,所以![]() .
.
因为![]() ,所以
,所以![]() .
.
又![]() ,故
,故![]()
(2)由(1)知![]() ,
, ![]() ,又
,又![]() ,交线为
,交线为![]() ,
,
所以![]() ,故
,故![]() 两两相互垂直.
两两相互垂直.
以![]() 为坐标原点,
为坐标原点, ![]() 的方向为
的方向为![]() 轴的正方向,
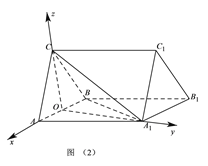
轴的正方向, ![]() 为单位长,建立如图(2)所示的空间直角坐标系
为单位长,建立如图(2)所示的空间直角坐标系![]() .由题设知
.由题设知![]() ,
,
则![]() ,
, ![]() ,
, ![]() .
.
设![]() 是平面
是平面![]() 的法向量,
的法向量,
则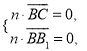 即
即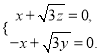 可取
可取![]() 故
故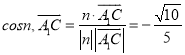 .
.
所以![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某班一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,其中,频率分布直方图的分组区间分别为[50,60),[60,70),[70,80),[80,90),[90,100],据此解答如下问题.
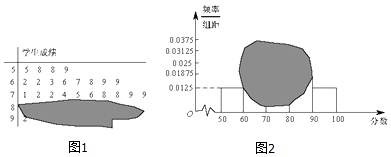
(Ⅰ)求全班人数及分数在[80,100]之间的频率;
(Ⅱ)现从分数在[80,100]之间的试卷中任取 3 份分析学生情况,设抽取的试卷分数在[90,100]的份数为X,求X的分布列和数学望期. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
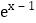 +ax,aR,
+ax,aR,(1)讨论函数f(x)的单调区间;
(2)求证:
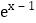 ≥x;
≥x;(3)求证:当a≥-2时,x[1,+ ∞),f(x)+lnx≥a+1恒成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
,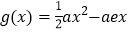 (
( ,
, 是自然对数的底数).
是自然对数的底数).(1)求函数
 的单调区间;
的单调区间;(2)若
 ,当
,当 时,求函数
时,求函数 的最大值;
的最大值;(3)若
 ,且
,且 ,比较:
,比较: 与
与 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△
 内接于圆
内接于圆 ,
, 是圆
是圆 的直径,四边形
的直径,四边形 为平行四边形,
为平行四边形, 平面
平面 ,
, .
.
(1)求证:
 ⊥平面
⊥平面 ;
;(2)设
 ,
,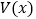 表示三棱锥
表示三棱锥 的体积,求函数
的体积,求函数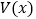 的解析式及最大值.
的解析式及最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,若m<n,且f(m)=f(n),则n﹣m的取值范围是( )
,若m<n,且f(m)=f(n),则n﹣m的取值范围是( )
A.[3﹣2ln2,2)
B.[3﹣2ln2,2]
C.[e﹣1,2]
D.[e﹣1,2) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,∠BCD=135°,侧面PAB⊥底面ABCD,∠BAP=90°,AB=AC=PA=2,E,F分别为BC,AD的中点,点M在线段PD上. (Ⅰ)求证:EF⊥平面PAC;
(Ⅱ)如果直线ME与平面PBC所成的角和直线ME与平面ABCD所成的角相等,求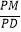 的值.
的值.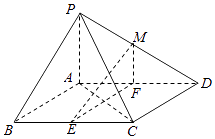
相关试题

