【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)求证:函数![]() 和
和![]() 在公共定义域内,
在公共定义域内,![]() 恒成立;
恒成立;
(3)若存在两个不同的实数![]() ,
,![]() ,满足
,满足![]() ,求证:
,求证:![]() .
.
参考答案:
【答案】(1)增区间为![]() ,减区间为
,减区间为![]() ;(2)证明见解析;(3)证明见解析.
;(2)证明见解析;(3)证明见解析.
【解析】分析:(1)构造函数![]() ,对函数求导,得到得到导函数的正负,进而得到单调区间和极值;(2)构造函数
,对函数求导,得到得到导函数的正负,进而得到单调区间和极值;(2)构造函数![]() ,对函数
,对函数![]() 和
和![]() 求导研究函数的单调性进而得到函数的最值,使得最小值大于2即可;(3)要证原式只需要证
求导研究函数的单调性进而得到函数的最值,使得最小值大于2即可;(3)要证原式只需要证![]() ,
,![]() 故得到即证:
故得到即证:![]() ,变量集中设
,变量集中设![]() 即可,转化为关于t的不等式.
即可,转化为关于t的不等式.
详解:
(1)函数![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
故当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
故函数![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() ;
;
(2)证明:函数![]() 和
和![]() 的公共定义域为
的公共定义域为![]() ,
,
![]() ,
,
设![]() ,则
,则![]() 在
在![]() 上单调递增,故
上单调递增,故![]() ;
;
设![]() ,当
,当![]() 时有极大值点,
时有极大值点,
![]() ;故
;故![]() ;
;
故函数![]() 和
和![]() 在公共定义域内,
在公共定义域内,![]() .
.
(3)证明:不妨设![]() ,由题意得,
,由题意得,
![]() ,
,![]() ;所以
;所以![]() ;
;
而要证![]() ,只需证明
,只需证明![]() ;
;
即证明![]() ;即证明
;即证明![]() ;
;
即证明, ;令
;令![]() ,则
,则![]() ;
;
即证明 ;设
;设![]() ;
;
则![]() ,故函数
,故函数![]() 在区间
在区间![]() 上是增函数,
上是增函数,
所以![]() ,即
,即![]() ;所以不等式
;所以不等式![]() 成立.
成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱
 中,
中,  .
.(Ⅰ)证明:
 ;
;(Ⅱ)平面

 平面
平面 ,
,  ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三点
 ,
, ,
, ,曲线
,曲线 上任意一点
上任意一点 满足
满足 .
.(1)求
 的方程;
的方程;(2)动点

 在曲线
在曲线 上,
上, 是曲线
是曲线 在
在 处的切线.问:是否存在定点
处的切线.问:是否存在定点 使得
使得 与
与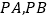 都相交,交点分别为
都相交,交点分别为 ,且
,且 与
与 的面积之比为常数?若存在,求
的面积之比为常数?若存在,求 的值;若不存在,说明理由.
的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于定义域为R的函数f(x),若满足①f(0)=0;②当x∈R,且x≠0时,都有xf'(x)>0;③当x1≠x2 , 且f(x1)=f(x2)时,x1+x2<0,则称f(x)为“偏对称函数”. 现给出四个函数:g(x)=
 ;φ(x)=ex﹣x﹣1.
;φ(x)=ex﹣x﹣1.
则其中是“偏对称函数”的函数个数为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且B=60°,c=4.
(Ⅰ)若b=6,求角C的正弦值及△ABC的面积;
(Ⅱ)若D,E在线段BC上,且BD=DE=EC, ,求AD的长.
,求AD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,侧面PAD⊥底面ABCD,底面ABCD是平行四边形,∠ABC=45°,AD=AP=2,
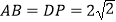 ,E为CD的中点,点F在线段PB上.
,E为CD的中点,点F在线段PB上. 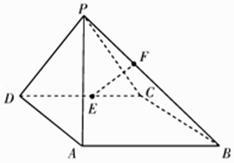
(Ⅰ)求证:AD⊥PC;
(Ⅱ)试确定点F的位置,使得直线EF与平面PDC所成的角和直线EF与平面ABCD所成的角相等. -
科目: 来源: 题型:
查看答案和解析>>【题目】某地区有小学21所,中学14所,大学7所,现采取分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查。
(I)求应从小学、中学、大学中分别抽取的学校数目。
(II)若从抽取的6所学校中随机抽取2所学校做进一步数据分析,
(1)列出所有可能的抽取结果;
(2)求抽取的2所学校均为小学的概率。
相关试题

