搜索
【题目】
中，角A，B,C的对边分别是
且满足
(1)求角B的大小；
(2)若的面积为为
，求
的值.
参考答案：
【答案】(1)
. ⑵a＋c＝
．
【解析】
本试题主要是考查了解三角形中正弦定理和余弦定理的综合运用，求解边和角的关系，同时也考查了三角形面积公式的运用。
（1）因为根据已知中的边角关系可以将边化为角，运用正弦定理，得到角的关系式，得到B。
（2）利用正弦面积公式可知，ac的乘积，然后再结合余弦定理可知a+c的值。
(1)因为
,
由正弦定理,得
, …………3分
即
.
在△ABC中，
，
，所以
.……………………………6分
又因为
，故. …………………………………………………… 7分
⑵ 因为△
的面积为
，所以
，所以
． ……………10分
因为b＝
，
，所以
＝3，即
＝3．
所以
＝12，所以a＋c＝． ……………………………………………14分
-
科目： 来源： 题型：
查看答案和解析>>【题目】若对任意的正整数
，总存在正整数
，使得数列
的前项和
，则称是“回归数列”.（1）①前
项和为
的数列是否是“回归数列”?并请说明理由；②通项公式为
的数列
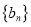是否是“回归数列”?并请说明理由；（2）设
是等差数列，首项
，公差
，若是“回归数列”，求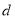
的值；（3）是否对任意的等差数列
，总存在两个“回归数列”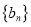和
，使得
成立，请给出你的结论，并说明理由. -
科目： 来源： 题型：
查看答案和解析>>【题目】以下茎叶图记录了甲，乙两组各四名同学单位时间内引体向上的次数，乙组记录中有一个数据模糊，无法确认，在图中以
表示.
（1）如果
，求乙组同学单位时间内引体向上次数的平均数和方差；（2）如果
，分别从甲，乙两组中随机选取一名同学，求这两名同学单位时间内引体向上次数和为19的概率.（注：方差
，其中
为
的平均数）. -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数
.（1）若函数
的最大值是最小值的
倍，求实数
的值；（2）若函数
存在零点，求函数的零点. -
科目： 来源： 题型：
查看答案和解析>>【题目】某市电视台为了宣传举办问答活动，随机对该市15～65岁的人群抽样了
人，回答问题计结果如下图表所示：
（1）分别求出
的值；（2）从第2，3，4组回答正确的人中用分层抽样的方法抽取6人，则第2，3，4组每组各抽取多少人？
（3）在（2）的前提下，电视台决定在所抽取的6人中随机抽取2人颁发幸运奖，求所抽取的人中第2组至少有1人获得幸运奖的概率.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某手机厂商推出一款6吋大屏手机，现对500名该手机用户（200名女性，300名男性）进行调查，对手机进行评分，评分的频数分布表如下：
女性用户
分值区间
[50，60）
[60，70）
[70，80）
[80，90）
[90，100]
频数
20
40
80
50
10
男性用户
分值区间
[50，60）
[60，70）
[70，80）
[80，90）
[90，100]
频数
45
75
90
60
30
（Ⅰ）完成下列频率分布直方图，并指出女性用户和男性用户哪组评分更稳定（不计算具体值，给出结论即可）；
（Ⅱ）根据评分的不同，运用分层抽样从男性用户中抽取20名用户，在这20名用户中，从评分不低于80分的用户中任意抽取3名用户，求3名用户中评分小于90分的人数的分布列和期望． -
科目： 来源： 题型：
查看答案和解析>>【题目】 某汽车租赁公司为了调查A, B两种车型的出租情况，现随机抽取这两种车型各50辆，分别统计了每辆车在某个星期内的出租天数，统计数据如下表:
A型车
出租天数
3
4
5
6
7
车辆数
3
30
5
7
5
B型车
出租天数
3
4
5
6
7
车辆数
10
10
15
10
5
(1)试根据上面的统计数据，判断这两种车型在本星期内出租天数的方差的大小关系(只需写出结果);
(2)现从出租天数为3天的汽车(仅限A, B两种车型)中随机抽取一辆，试估计这辆汽车是A型车的概率;
(3)如果两种车型每辆车每天出租获得的利润相同，该公司需要购买一辆汽车，请你根据所学的统计知识，给出建议应该购买哪一种车型，并说明你的理由．
相关试题
