【题目】以下茎叶图记录了甲,乙两组各四名同学单位时间内引体向上的次数,乙组记录中有一个数据模糊,无法确认,在图中以![]() 表示.
表示.

(1)如果![]() ,求乙组同学单位时间内引体向上次数的平均数和方差;
,求乙组同学单位时间内引体向上次数的平均数和方差;
(2)如果![]() ,分别从甲,乙两组中随机选取一名同学,求这两名同学单位时间内引体向上次数和为19的概率.
,分别从甲,乙两组中随机选取一名同学,求这两名同学单位时间内引体向上次数和为19的概率.
(注:方差![]() ,其中
,其中![]() 为
为![]() 的平均数).
的平均数).
参考答案:
【答案】(1)平均数![]() ,方差
,方差![]() (2)
(2)![]()
【解析】
(1)根据平均数和方差计算公式直接求得结果;(2)首先确定在甲、乙两组随机选取一名同学的所有情况,再找到次数和为![]() 的情况,根据古典概型求得结果.
的情况,根据古典概型求得结果.
(1)当![]() 时,由茎叶图可知,乙组同学的引体向上次数是
时,由茎叶图可知,乙组同学的引体向上次数是![]() ,
,![]() ,
,![]() ,
,![]()
![]() 平均数为:
平均数为:![]()
方差为: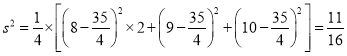
(2)记甲组四名同学分别为![]() ,
,![]() ,
,![]() ,
,![]() ,引体向上的次数依次为
,引体向上的次数依次为![]() ,
,![]() ,
,![]() ,
,![]() ;
;
乙组四名同学分别为![]() ,
,![]() ,
,![]() ,
,![]() ,他们引体向上的次数依次为
,他们引体向上的次数依次为![]() ,
,![]() ,
,![]() ,
,![]()
分别从甲、乙两组中随机选取一名同学,所有可能的结果有![]() 个,即:
个,即:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
用![]() 表示“选出的两名同学的引体向上次数和为
表示“选出的两名同学的引体向上次数和为![]() ”这一事件
”这一事件
则![]() 中的结果有
中的结果有![]() 个,它们是:
个,它们是:![]() ,
,![]() ,
,![]() ,
,![]()
故所求概率:![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
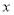 的一元二次方程
的一元二次方程 .
.(1)若
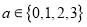 ,
, ,求方程
,求方程 有实根的概率;
有实根的概率;(2)若
 ,
, ,求方程
,求方程 有实根的概率.
有实根的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】(题文)已知函数
 .
.(Ⅰ)若
 在区间
在区间 上单调递增,求实数
上单调递增,求实数 的取值范围;
的取值范围;(Ⅱ)若存在唯一整数
 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】若对任意的正整数
 ,总存在正整数
,总存在正整数 ,使得数列
,使得数列 的前
的前 项和
项和 ,则称
,则称 是“回归数列”.
是“回归数列”.(1)①前
 项和为
项和为 的数列
的数列 是否是“回归数列”?并请说明理由;
是否是“回归数列”?并请说明理由;②通项公式为
 的数列
的数列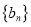 是否是“回归数列”?并请说明理由;
是否是“回归数列”?并请说明理由;(2)设
 是等差数列,首项
是等差数列,首项 ,公差
,公差 ,若
,若 是“回归数列”,求
是“回归数列”,求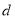 的值;
的值;(3)是否对任意的等差数列
 ,总存在两个“回归数列”
,总存在两个“回归数列”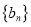 和
和 ,使得
,使得 成立,请给出你的结论,并说明理由.
成立,请给出你的结论,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)若函数
 的最大值是最小值的
的最大值是最小值的 倍,求实数
倍,求实数 的值;
的值;(2)若函数
 存在零点,求函数的零点.
存在零点,求函数的零点. -
科目: 来源: 题型:
查看答案和解析>>【题目】
 中,角A,B,C的对边分别是
中,角A,B,C的对边分别是 且满足
且满足
(1)求角B的大小;
(2)若
 的面积为为
的面积为为 ,求
,求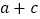 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市电视台为了宣传举办问答活动,随机对该市15~65岁的人群抽样了
 人,回答问题计结果如下图表所示:
人,回答问题计结果如下图表所示:
(1)分别求出
 的值;
的值;(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,则第2,3,4组每组各抽取多少人?
(3)在(2)的前提下,电视台决定在所抽取的6人中随机抽取2人颁发幸运奖,求所抽取的人中第2组至少有1人获得幸运奖的概率.
相关试题

