搜索
【题目】已知函数
.
（1）若函数
的最大值是最小值的
倍，求实数
的值；
（2）若函数存在零点，求函数的零点.
参考答案：
【答案】（1）
或
或
或
.（2）当
时，零点为
；当
时，零点为
【解析】
（1）将
整理为
，换元可得
，
；根据对称轴位置的不同，分别在
，
，
和
四种情况下构造最大值和最小值关系的方程，解方程求得结果；（2）根据（1）中最值的取值范围可知若存在零点，必有或
，从而可知
的取值，进而得到零点.
（1）
当
时，
，令
，
①当时，
，
；
有
，解得：
或
由得：
②当时，
，
；
有
，解得：
或
由得：
③当时，
，；
有
，解得：
由得：
④当时，，
有
，解得：
由得：
综上所述：或或或
（2）由（1）知，
，
，
若函数存在零点，则必有：或
①当时，
，此时函数的零点为：；
②当时，
，此时函数的零点为：
-
科目： 来源： 题型：
查看答案和解析>>【题目】（题文）已知函数
.（Ⅰ）若
在区间
上单调递增，求实数
的取值范围；（Ⅱ）若存在唯一整数
，使得
成立，求实数的取值范围. -
科目： 来源： 题型：
查看答案和解析>>【题目】若对任意的正整数
，总存在正整数
，使得数列
的前项和
，则称是“回归数列”.（1）①前
项和为
的数列是否是“回归数列”?并请说明理由；②通项公式为
的数列
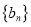是否是“回归数列”?并请说明理由；（2）设
是等差数列，首项
，公差
，若是“回归数列”，求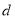
的值；（3）是否对任意的等差数列
，总存在两个“回归数列”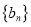和
，使得
成立，请给出你的结论，并说明理由. -
科目： 来源： 题型：
查看答案和解析>>【题目】以下茎叶图记录了甲，乙两组各四名同学单位时间内引体向上的次数，乙组记录中有一个数据模糊，无法确认，在图中以
表示.
（1）如果
，求乙组同学单位时间内引体向上次数的平均数和方差；（2）如果
，分别从甲，乙两组中随机选取一名同学，求这两名同学单位时间内引体向上次数和为19的概率.（注：方差
，其中
为
的平均数）. -
科目： 来源： 题型：
查看答案和解析>>【题目】
中，角A，B,C的对边分别是
且满足
(1)求角B的大小；
(2)若
的面积为为
，求
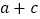的值. -
科目： 来源： 题型：
查看答案和解析>>【题目】某市电视台为了宣传举办问答活动，随机对该市15～65岁的人群抽样了
人，回答问题计结果如下图表所示：
（1）分别求出
的值；（2）从第2，3，4组回答正确的人中用分层抽样的方法抽取6人，则第2，3，4组每组各抽取多少人？
（3）在（2）的前提下，电视台决定在所抽取的6人中随机抽取2人颁发幸运奖，求所抽取的人中第2组至少有1人获得幸运奖的概率.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某手机厂商推出一款6吋大屏手机，现对500名该手机用户（200名女性，300名男性）进行调查，对手机进行评分，评分的频数分布表如下：
女性用户
分值区间
[50，60）
[60，70）
[70，80）
[80，90）
[90，100]
频数
20
40
80
50
10
男性用户
分值区间
[50，60）
[60，70）
[70，80）
[80，90）
[90，100]
频数
45
75
90
60
30
（Ⅰ）完成下列频率分布直方图，并指出女性用户和男性用户哪组评分更稳定（不计算具体值，给出结论即可）；
（Ⅱ）根据评分的不同，运用分层抽样从男性用户中抽取20名用户，在这20名用户中，从评分不低于80分的用户中任意抽取3名用户，求3名用户中评分小于90分的人数的分布列和期望．
相关试题
