【题目】若对任意的正整数![]() ,总存在正整数
,总存在正整数![]() ,使得数列
,使得数列![]() 的前
的前![]() 项和
项和![]() ,则称
,则称![]() 是“回归数列”.
是“回归数列”.
(1)①前![]() 项和为
项和为![]() 的数列
的数列![]() 是否是“回归数列”?并请说明理由;
是否是“回归数列”?并请说明理由;
②通项公式为![]() 的数列
的数列![]() 是否是“回归数列”?并请说明理由;
是否是“回归数列”?并请说明理由;
(2)设![]() 是等差数列,首项
是等差数列,首项![]() ,公差
,公差![]() ,若
,若![]() 是“回归数列”,求
是“回归数列”,求![]() 的值;
的值;
(3)是否对任意的等差数列![]() ,总存在两个“回归数列”
,总存在两个“回归数列”![]() 和
和![]() ,使得
,使得![]() 成立,请给出你的结论,并说明理由.
成立,请给出你的结论,并说明理由.
参考答案:
【答案】(1)①是;②是;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)①利用公式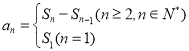 和
和 ![]() ,求出数列
,求出数列![]() 的通项公式,按照回归数列的定义进行判断;
的通项公式,按照回归数列的定义进行判断;
②求出数列![]() 的前
的前![]() 项和,按照回归数列的定义进行判断;
项和,按照回归数列的定义进行判断;
(2)求出![]() 的前
的前![]() 项和,根据
项和,根据![]() 是“回归数列”,可得到等式,通过取特殊值,求出
是“回归数列”,可得到等式,通过取特殊值,求出![]() 的值;
的值;
(3)等差数列![]() 的公差为
的公差为![]() ,构造数列
,构造数列![]() ,可证明
,可证明
![]() 、
、![]() 是等差数列,再利用等差数列前
是等差数列,再利用等差数列前![]() 项和,及其通项公式,回归数列的概念,即可求出.
项和,及其通项公式,回归数列的概念,即可求出.
(1)①当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,![]() ,所以数列
,所以数列![]() 是“回归数列”;
是“回归数列”;
②因为![]() ,所以前n项和
,所以前n项和![]() ,根据题意
,根据题意![]() ,
,
因为![]() 一定是偶数,所以存在
一定是偶数,所以存在![]() ,使得
,使得![]() ,
,
所以数列{![]() }是“回归数列”;
}是“回归数列”;
(2)设![]() 是等差数列为
是等差数列为![]() ,由题意可知:对任意的正整数
,由题意可知:对任意的正整数![]() ,总存在正整数
,总存在正整数![]() ,使得数列
,使得数列![]() 的前
的前![]() 项和
项和![]() ,即
,即![]() ,取
,取![]() ,得
,得![]() ,解得
,解得![]() ,公差
,公差![]() ,所以
,所以![]() ,又
,又![]() ;
;
(3)设等差数列![]() =
=![]() ,
,
总存在两个回归数列![]() ,显然
,显然![]() 和
和![]() 是等差数列,使得
是等差数列,使得![]() ,
,
证明如下:![]() ,
,
数列{![]() }前n项和
}前n项和![]() ,
,![]()
![]() 时,
时,![]() 为正整数,当
为正整数,当![]() 时,
时,![]() ,
,
所以存在正整数![]() ,使得
,使得![]() ,所以{
,所以{![]() }是“回归数列”,
}是“回归数列”,
数列{![]() }前n项和
}前n项和![]()
![]() ,存在正整数
,存在正整数![]() ,使得
,使得![]() ,所以{
,所以{![]() }是“回归数列”,所以结论成立.
}是“回归数列”,所以结论成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
 中,曲线
中,曲线 的参数方程为
的参数方程为 (
(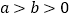 ,
, 为参数),在以
为参数),在以 为极点,
为极点, 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线 是圆心在极轴上,且经过极点的圆.已知曲线
是圆心在极轴上,且经过极点的圆.已知曲线 上的点
上的点 对应的参数
对应的参数 ,射线
,射线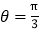 与曲线
与曲线 交于点
交于点 .
.(Ⅰ)求曲线
 ,
, 的标准方程;
的标准方程;(Ⅱ)若点
 ,
, 在曲线
在曲线 上,求
上,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
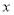 的一元二次方程
的一元二次方程 .
.(1)若
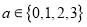 ,
, ,求方程
,求方程 有实根的概率;
有实根的概率;(2)若
 ,
, ,求方程
,求方程 有实根的概率.
有实根的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】(题文)已知函数
 .
.(Ⅰ)若
 在区间
在区间 上单调递增,求实数
上单调递增,求实数 的取值范围;
的取值范围;(Ⅱ)若存在唯一整数
 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】以下茎叶图记录了甲,乙两组各四名同学单位时间内引体向上的次数,乙组记录中有一个数据模糊,无法确认,在图中以
 表示.
表示.
(1)如果
 ,求乙组同学单位时间内引体向上次数的平均数和方差;
,求乙组同学单位时间内引体向上次数的平均数和方差;(2)如果
 ,分别从甲,乙两组中随机选取一名同学,求这两名同学单位时间内引体向上次数和为19的概率.
,分别从甲,乙两组中随机选取一名同学,求这两名同学单位时间内引体向上次数和为19的概率.(注:方差
 ,其中
,其中 为
为 的平均数).
的平均数). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)若函数
 的最大值是最小值的
的最大值是最小值的 倍,求实数
倍,求实数 的值;
的值;(2)若函数
 存在零点,求函数的零点.
存在零点,求函数的零点. -
科目: 来源: 题型:
查看答案和解析>>【题目】
 中,角A,B,C的对边分别是
中,角A,B,C的对边分别是 且满足
且满足
(1)求角B的大小;
(2)若
 的面积为为
的面积为为 ,求
,求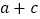 的值.
的值.
相关试题

