【题目】已知四棱锥P﹣ABCD中,底面为矩形,PA⊥底面ABCD,PA=BC=1,AB=2,M为PC中点.
(Ⅰ)在图中作出平面ADM与PB的交点N,并指出点N所在位置(不要求给出理由);
(Ⅱ)在线段CD上是否存在一点E,使得直线AE与平面ADM所成角的正弦值为 ![]() ,若存在,请说明点E的位置;若不存在,请说明理由;
,若存在,请说明点E的位置;若不存在,请说明理由;
(Ⅲ)求二面角A﹣MD﹣C的余弦值.
参考答案:
【答案】解:(Ⅰ)过M作MN∥BC,交PB于点N,连接AN,如图,
则点N为平面ADM与PB的交点N(在图中画出)
由M为PC中点,得N为PB的中点.
(Ⅱ)因为四棱锥P﹣ABCD中,底面为矩形,PA⊥底面ABCD,
以A为坐标原点,以直线AB,AD,AP所在直线建立空间直角坐标系如图所示:
则A(0,0,0),P(0,0,1),D(0,1,0),C(2,1,0),M(1, ![]() ),
),
设在线段CD上存在一点E(x,1,0),则 ![]()
设直线AE与平面AMD所成角为θ,平面AMD的法向量为 ![]() ,
,
则 ![]() ,即
,即  ,令z=2,则
,令z=2,则 ![]() ,
,
因为直线AE与平面ADM所成角的正弦值为 ![]() ,
,
所以  ,所以x=1
,所以x=1
所以在线段CD上存在中点E,
使得直线AE与平面AMD所成角的正弦值为 ![]()
(Ⅲ)设平面CMD的法向量 ![]() ,
,
则 ![]() ,即
,即  ,令z′=﹣1,则y′=﹣1,
,令z′=﹣1,则y′=﹣1,
所以 ![]()
所以  ,
,
由图形知二面角A﹣MD﹣C的平面角是钝角,
所以二面角A﹣MD﹣C的平面角的余弦值为 ![]()

【解析】(Ⅰ)过M作MN∥BC,交PB于点N,由此求出结果.(Ⅱ)以A为坐标原点,以直线AB,AD,AP所在直线建立空间直角坐标系,利用向量法能求出在线段CD上存在中点E,使得直线AE与平面AMD所成角的正弦值为 ![]() .(Ⅲ)求出平面CMD的法向量和平面AMD的法向量,由此利用向量法能求出二面角A﹣MD﹣C的平面角的余弦值.
.(Ⅲ)求出平面CMD的法向量和平面AMD的法向量,由此利用向量法能求出二面角A﹣MD﹣C的平面角的余弦值.
【考点精析】掌握直线与平面垂直的判定是解答本题的根本,需要知道一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
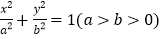 与
与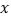 轴,
轴,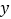 轴的正半轴分别交于A,B两点,原点O到直线AB的距离为
轴的正半轴分别交于A,B两点,原点O到直线AB的距离为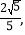 该椭圆的离心率为
该椭圆的离心率为
(1)求椭圆的方程
(2)是否存在过点P(
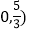 的直线
的直线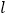 与椭圆交于M,N两个不同的点,使
与椭圆交于M,N两个不同的点,使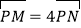 成立?若存在,求出
成立?若存在,求出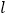 的方程;若不存在,说明理由。
的方程;若不存在,说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】据《中国新闻网》10月21日报道,全国很多省市将英语考试作为高考改革的重点,一时间“英语考试该如何改”引起广泛关注.为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3600人调查,就是否“取消英语听力”的问题,调查统计的结果如下表:
态度
调查人群应该取消
应该保留
无所谓
在校学生
2100人
120人
y人
社会人士
600人
x人
z人
已知在全体样本中随机抽取1人,抽到持“应该保留”态度的人的概率为0.05.
(Ⅰ)现用分层抽样的方法在所有参与调查的人中抽取360人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(Ⅱ)在持“应该保留”态度的人中,用分层抽样的方法抽取6人平均分成两组进行深入交流,求第一组中在校学生人数ξ的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】正四面体ABCD中,M是棱AD的中点,O是点A在底面BCD内的射影,则异面直线BM与AO所成角的余弦值为____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
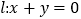 ,求:
,求:(1)点P(4,5)关于l的对称点;
(2)直线x-y-2=0关于直线l对称的直线方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知O为坐标原点,抛物线C:y2=nx(n>0)在第一象限内的点P(2,t)到焦点的距离为
 ,曲线C在点P处的切线交x轴于点Q,直线l1经过点Q且垂直于x轴.
,曲线C在点P处的切线交x轴于点Q,直线l1经过点Q且垂直于x轴.
(Ⅰ)求线段OQ的长;
(Ⅱ)设不经过点P和Q的动直线l2:x=my+b交曲线C于点A和B,交l1于点E,若直线PA,PE,PB的斜率依次成等差数列,试问:l2是否过定点?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P-ABCD中,底面ABCD是正方形.点E是棱PC的中点,平面ABE与棱PD交于点F.

(1)求证:AB∥EF;
(2)若PA=AD,且平面PAD⊥平面ABCD,求证:AF⊥平面PCD.
相关试题

