【题目】已知函数![]() (
(![]() ).
).
(Ⅰ)试判断函数![]() 的零点个数;
的零点个数;
(Ⅱ)若函数![]() 在
在![]() 上为增函数,求整数
上为增函数,求整数![]() 的最大值.
的最大值.
(可能要用的数据: ![]() ,
, ![]() ,
, ![]() ).
).
参考答案:
【答案】(1)见解析(2)6
【解析】试题分析: (1)对函数![]() 求导,由
求导,由![]() 在
在![]() 恒成立,则
恒成立,则![]() 在
在![]() 上为增函数,由
上为增函数,由![]() ,
, ![]() 可判断出函数有唯一零点; (2)对函数
可判断出函数有唯一零点; (2)对函数![]() 求导,分离参变量,
求导,分离参变量, ![]() 在
在![]() 上恒成立,构造新函数
上恒成立,构造新函数![]() 求导,由(1)可知,a小于等于
求导,由(1)可知,a小于等于![]() 在区间
在区间![]() 上的最小值,根据函数的单调性,求得函数
上的最小值,根据函数的单调性,求得函数![]() 最小值的取值范围,即可取得整数a的最大值.
最小值的取值范围,即可取得整数a的最大值.
试题解析:解:(Ⅰ) ![]() 在
在![]() 上为增函数,
上为增函数,
且![]() ,故
,故![]() 在
在![]() 上为增函数,
上为增函数,
又![]() ,
, ![]() ,
,
则函数![]() 在
在![]() 上有唯一零点.
上有唯一零点.
(Ⅱ)![]() 在
在![]() 上恒成立,
上恒成立,
当![]() 时显然成立,
时显然成立,
当![]() 时,可得
时,可得![]() 在
在![]() 上恒成立,
上恒成立,
令![]() ,则
,则![]() ,
, ![]() ,
,
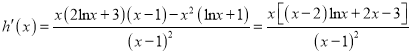 ,
,
由(Ⅰ)可知: ![]() 在
在![]() 上为增函数,故
上为增函数,故![]() 在
在![]() 上有唯一零点
上有唯一零点![]() ,
,
则![]() 在区间
在区间![]() 上为减函数,
上为减函数,
![]() 在区间
在区间![]() 上为增函数,
上为增函数,
故![]() 时,
时, ![]() 有最小值,
有最小值, ![]()
![]() .
.
又![]() ,
,
![]() ,
,
则![]() ,
,
有![]() ,
,
所以![]() ,
, ![]() ,
,
令![]() ,则
,则![]() 最小值
最小值
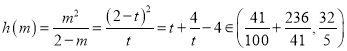 ,
,
因![]() ,则
,则![]() 的最小值大约在
的最小值大约在![]() 之间,
之间,
故整数![]() 的最大值为6.
的最大值为6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,甲船以每小时30
 海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的南偏西75°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的南偏西60°方向的B2处,此时两船相距10
海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的南偏西75°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的南偏西60°方向的B2处,此时两船相距10 海里.问:乙船每小时航行多少海里?
海里.问:乙船每小时航行多少海里?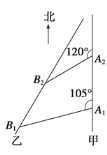
-
科目: 来源: 题型:
查看答案和解析>>【题目】设等差数列{an}满足a3=5,a10=-9.
(1)求{an}的通项公式;
(2)求{an}的前n项和Sn及使得Sn最大的序号n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:在数列
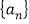 中,若
中,若 为常数)则称
为常数)则称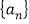 为“等方差数列”,下列是对“等方差数列”的有关判断( )
为“等方差数列”,下列是对“等方差数列”的有关判断( )①若
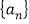 是“等方差数列”,在数列
是“等方差数列”,在数列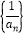 是等差数列;
是等差数列;②
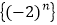 是“等方差数列”;
是“等方差数列”;③若
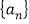 是“等方差数列”,则数列
是“等方差数列”,则数列 为常)也是“等方差数列”;
为常)也是“等方差数列”;④若
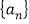 既是“等方差数列”又是等差数列,则该数列是常数数列.
既是“等方差数列”又是等差数列,则该数列是常数数列.其中正确命题的个数为( )
A.
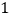 B.
B. 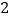 C.
C. 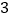 D.
D. 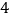
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知α∈
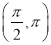 ,且sin
,且sin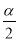 +cos
+cos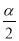 =
=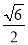 .
.(1)求cos α的值;
(2)若sin(α-β)=-
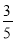 ,β∈
,β∈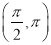 ,求cos β的值.
,求cos β的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】双“十一”结束之后,某网站针对购物情况进行了调查,参与调查的人主要集中在[20,50]岁之间,若规定:购物600(含600元)以下者,称为“理智购物”,购物超过600元者被网友形象的称为“剁手党”,得到如下统计表:
分组编号
年龄分组
球迷
所占比例
1
[20,25)
1000
0.5
2
[25,30)
1800
0.6
3
[30,35)
1200
0.5
4
[35,40)
a
0.4
5
[40,45)
300
0.2
6
[45,50]
200
0.1
若参与调查的“理智购物”总人数为7720人.
(1)求a的值;
(2)从年龄在[20,35)的“剁手党”中按照年龄区间分层抽样的方法抽取20人; ①从这20人中随机抽取2人,求这2人恰好属于同一年龄区间的概率;
②从这20人中随机抽取2人,用ζ表示年龄在[20,25)之间的人数,求ξ的分布列及期望值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
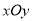 中,
中, 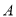 ,
, 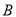 两点的坐标分别为
两点的坐标分别为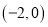 ,
, 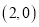 ,动点
,动点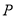 满足:直线
满足:直线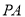 与直线
与直线 的斜率之积为
的斜率之积为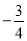 .
.(Ⅰ)求动点
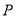 的轨迹
的轨迹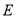 的方程;
的方程;(Ⅱ)过点
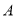 作两条互相垂直的直线
作两条互相垂直的直线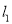 ,
, 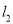 分别交曲线
分别交曲线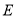 于
于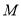 ,
, 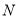 两点,设
两点,设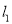 的斜率为
的斜率为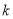 (
(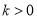 ),
),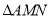 的面积为
的面积为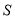 ,求
,求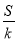 的取值范围.
的取值范围.
相关试题

