【题目】已知数列![]() 满足
满足![]() .
.
(1)求证:数列![]() 是等比数列,并求
是等比数列,并求![]() 的通项公式;
的通项公式;
(2)记数列![]() 的前
的前![]() 项和
项和![]() ,求使得
,求使得![]() 成立的最小整数
成立的最小整数![]() .
.
参考答案:
【答案】(1)证明见解析,![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)由利用等比数列的定义证明即可,需要利用![]() 整理化简,数列
整理化简,数列![]() 就以
就以![]() 不首项,公比为
不首项,公比为![]() 的等比数列,由此能够求出数列
的等比数列,由此能够求出数列![]() 的通项公式;(2)利用分组求和法得
的通项公式;(2)利用分组求和法得![]() ,由眦能求出使得
,由眦能求出使得![]() 成立的最小整数.
成立的最小整数.
试题解析:(1)证明:∵![]() ,∴
,∴![]() ,
,
∴![]() 为常数,
为常数,
又![]() ,
,
∴![]() 是以3为首项,2为公比的等比数列,...........................3分
是以3为首项,2为公比的等比数列,...........................3分
∴![]() ,
,
∴![]() ,
,
叠加得![]() ,
,
∴![]() ,即
,即![]() ................6分
................6分
(2)由(1)得![]() ,
,
∴![]() ,..............10分
,..............10分
∴![]() ,即为
,即为![]() ,
,
∴![]() ,∵
,∵![]() ,
,
∴![]() ,∴最小整数
,∴最小整数![]() 为4............................12分
为4............................12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了整顿食品的安全卫生,食品监督部门对某食品厂生产甲、乙两种食品进行了检测调研,检测某种有害微量元素的含量,随机在两种食品中各抽取了10个批次的食品,每个批次各随机地抽取了一件,下表是测量数据的茎叶图(单位:毫克).

规定:当食品中的有害微量元素的含量在
 时为一等品,在
时为一等品,在 为二等品,20以上为劣质品.
为二等品,20以上为劣质品.(1)用分层抽样的方法在两组数据中各抽取5个数据,再分别从这5个数据中各选取2个,求甲的一等品数与乙的一等品数相等的概率;
(2)每生产一件一等品盈利50元,二等品盈利20元,劣质品亏损20元,根据上表统计得到甲、乙两种食品为一等品、二等品、劣质品的频率,分别估计这两种食品为一等品、二等品、劣质品的概率,若分别从甲、乙食品中各抽取1件,设这两件食品给该厂带来的盈利为
 ,求随机变量
,求随机变量 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】某高科技企业生产产品
 和产品
和产品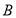 需要甲、乙两种新型材料,生产一件产品
需要甲、乙两种新型材料,生产一件产品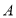 需要甲材料1.5
需要甲材料1.5 ,乙材料1
,乙材料1 ,用5个工时,生产一件产品需要甲材料0.5
,用5个工时,生产一件产品需要甲材料0.5 ,乙材料0.3
,乙材料0.3 ,用3个工时,生产一件产品的利润为2100元,生产一件产品的利润为900元.该企业现有甲材料150
,用3个工时,生产一件产品的利润为2100元,生产一件产品的利润为900元.该企业现有甲材料150 ,乙材料90
,乙材料90 ,则在不超过600个工时的条件下,生产产品
,则在不超过600个工时的条件下,生产产品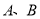 的利润之和的最大值为____________元.
的利润之和的最大值为____________元. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, ,
, .
.(1)当
 ,
, 时,求函数
时,求函数 的单调区间;
的单调区间;(2)当
 时,若
时,若 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;(3)设函数
 的图象在两点
的图象在两点 ,
, 处的切线分别为
处的切线分别为 ,
, ,若
,若 ,
, ,且
,且 ,求实数
,求实数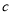 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,其中
,其中 ,
, .
. 是自然对数的底数.
是自然对数的底数.(1)求曲线
 在
在 处的切线方程为
处的切线方程为 ,求实数
,求实数 ,
, 的值;
的值;(2)①若
 时,函数
时,函数 既有极大值又有极小值,求实数
既有极大值又有极小值,求实数 的取值范围;
的取值范围;②若
 ,
, ,若
,若 对一切正实数
对一切正实数 恒成立,求实数
恒成立,求实数 的取值范围(用
的取值范围(用 表示).
表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知不等式
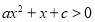 的解集为
的解集为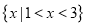 .
.(1)求
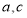 的值;
的值;(2)若不等式
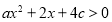 的解集为
的解集为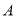 ,不等式
,不等式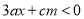 的解集为
的解集为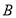 ,且
,且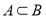 ,求实数
,求实数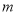 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( 为实数).
为实数).(1)当
 时,求函数
时,求函数 的图象在点
的图象在点 处的切线方程;
处的切线方程;(2)设函数
 (其中
(其中 为常数),若函数
为常数),若函数 在区间
在区间 上不存在极值,且存在
上不存在极值,且存在 满足
满足 ,求
,求 的取值范围;
的取值范围;(3)已知
 ,求证:
,求证: .
.
相关试题

