【题目】为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,下表记录了小李某月1号到5号每天打篮球时间![]() (单位:小时)与当天投篮命中率
(单位:小时)与当天投篮命中率![]() 之间的关系:
之间的关系:
时间 | 1 | 2 | 3 | 4 | 5 |
命中率 | 0.4 | 0.5 | 0.6 | 0.6 | 0.4 |
小李这5天的平均投篮命中率;用线性回归分析的方法,预测小李该月6号打6小时篮球的投篮命中率.
附:线性回归方程![]() 中系数计算公式
中系数计算公式 ,
, ![]() ,
,
参考答案:
【答案】预测小李该月6号打6小时篮球的投篮命中率为![]()
【解析】试题分析:(1)先求出小李这![]() 天的平均投篮命中率,从而可得样本中心点的坐标,利用
天的平均投篮命中率,从而可得样本中心点的坐标,利用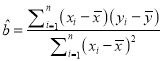 求出
求出![]() ,样本中心点的坐标代入回归方程可求得
,样本中心点的坐标代入回归方程可求得![]() ,进而求出线性回归方程,先再令
,进而求出线性回归方程,先再令![]() ,即可预测小李该月
,即可预测小李该月![]() 号打
号打![]() 小时篮球的投篮命中率.
小时篮球的投篮命中率.
试题解析:小李这5天的平均投篮命中率
![]() ,
,![]() ,
,
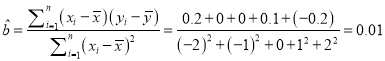 ,
, ![]()
∴线性回归方程![]() ,则当
,则当![]() 时,
时, ![]()
∴预测小李该月6号打6小时篮球的投篮命中率为![]() .
.
【方法点晴】本题主要考查散点图的画法和线性回归方程,属于难题.求回归直线方程的步骤:①依据样本数据画出散点图,确定两个变量具有线性相关关系;②计算![]() 的值;③计算回归系数
的值;③计算回归系数![]() ;④写出回归直线方程为
;④写出回归直线方程为![]() ;(2) 回归直线过样本点中心
;(2) 回归直线过样本点中心![]() 是一条重要性质,利用线性回归方程可以估计总体,帮助我们分析两个变量的变化趋势.
是一条重要性质,利用线性回归方程可以估计总体,帮助我们分析两个变量的变化趋势.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)是R上的奇函数,当x>0时,解析式为f(x)=
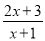 .
. (1)求f(x)在R上的解析式;
(2)用定义证明f(x)在(0,+∞)上为减函数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】祖暅原理:“幂势既同,则积不容异”.它是中国古代一个涉及几何体体积的问题,意思是两个同高的几何体,如在等高处的截面积恒相等,则体积相等.设
 为两个同高的几何体,
为两个同高的几何体,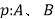 的体积不相等,
的体积不相等,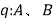 在等高处的截面积不恒相等,根据祖暅原理可知,
在等高处的截面积不恒相等,根据祖暅原理可知,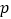 是
是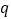 的( )
的( )A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
-
科目: 来源: 题型:
查看答案和解析>>【题目】设数列
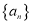 的前
的前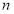 项和为
项和为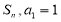 ,且对任意正整数
,且对任意正整数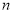 ,满足
,满足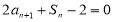 .
.(1)求数列
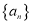 的通项公式.
的通项公式.(2)设
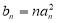 ,求数列
,求数列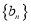 的前
的前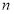 项和
项和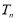 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
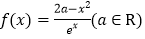 .
.(Ⅰ)求函数
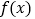 的单调区间;
的单调区间;(Ⅱ)若
 ,不等式
,不等式 恒成立,求实数
恒成立,求实数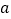 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线
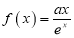 在
在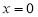 处的切线方程为
处的切线方程为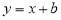 .
.(1)求
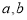 的值;
的值;(2)若对任意
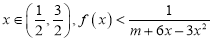 恒成立,求
恒成立,求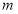 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】类比平面内正三角形的“三边相等,三内角相等”的性质,可推出正四面体的下列一些性质,你认为比较恰当的是( )
①各棱长相等,同一顶点上的任两条棱的夹角都相等;②各个面都是全等的正三角形,相邻两个面所成的二面角都相等;③各个面都是全等的正三角形,同一顶点上的任两条棱的夹角都相等。
A. ① B. ②③ C. ①② D. ①②③
相关试题

