【题目】已知f(x)是R上的奇函数,当x>0时,解析式为f(x)=![]() .
.
(1)求f(x)在R上的解析式;
(2)用定义证明f(x)在(0,+∞)上为减函数.
参考答案:
【答案】(1) f(x)=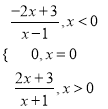 (2)见解析
(2)见解析
【解析】试题分析:(1)分别求出当x<0和x=0时的解析式,写成分段函数的形式;(2)设x1,x2∈(0,+∞),且x1<x2,通过作差证明f(x1)>f(x2)即可。
试题解析:(1)设x<0,则-x>0,
∴f(-x)=![]() .
.
又∵f(x)是R上的奇函数,
∴f(-x)=-f(x)=![]() ,
,
∴f(x)=![]() .
.
又∵奇函数在x=0时有意义,
∴f(0)=0,
∴函数的解析式为f(x)=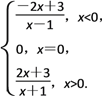
(2)证明:设x1,x2∈(0,+∞),且x1<x2,
则f(x1)-f(x2)=![]() -
-![]() =
=
![]()
=![]() .
.
∵x1,x2∈(0,+∞),x1<x2,
∴x1+1>0,x2+1>0,x2-x1>0,
∴f(x1)-f(x2)>0,
∴f(x1)>f(x2),
∴函数f(x)在(0,+∞)上为减函数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某科考试中,从甲、乙两个班级各抽取10名同学的成绩进行统计分析,两班成绩的茎叶图如图所示,成绩不小于90分为及格.
(Ⅰ)设甲、乙两个班所抽取的10名同学成绩方差分别为
 、
、 ,比较
,比较 、
、 的大小(直接写出结果,不写过程);
的大小(直接写出结果,不写过程);(Ⅱ)从甲班10人任取2人,设这2人中及格的人数为X,求X的分布列和期望;
(Ⅲ)从两班这20名同学中各抽取一人,在已知有人及格的条件下,求抽到乙班同学不及格的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,均值与方差都不变;
②设有一个回归方程
 ,变量x增加一个单位时,y平均增加3个单位;
,变量x增加一个单位时,y平均增加3个单位;③线性回归方程
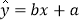 必经过点
必经过点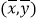 ;
;④在吸烟与患肺病这两个分类变量的计算中,从独立性检验知,有99%的把握认为吸烟与患肺病有关系时,我们说现有100人吸烟,那么其中有99人患肺病.其中错误的个数是( )
A. 0
B. 1
C. 2
D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】设全集U=R,集合A={x|-1≤x<3},B={x|2x-4≥x-2}.
(1)求U(A∩B);
(2)若集合C={x|2x+a>0},满足B∪C=C,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】祖暅原理:“幂势既同,则积不容异”.它是中国古代一个涉及几何体体积的问题,意思是两个同高的几何体,如在等高处的截面积恒相等,则体积相等.设
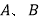 为两个同高的几何体,
为两个同高的几何体,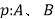 的体积不相等,
的体积不相等,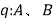 在等高处的截面积不恒相等,根据祖暅原理可知,
在等高处的截面积不恒相等,根据祖暅原理可知,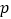 是
是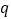 的( )
的( )A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
-
科目: 来源: 题型:
查看答案和解析>>【题目】设数列
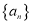 的前
的前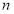 项和为
项和为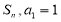 ,且对任意正整数
,且对任意正整数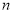 ,满足
,满足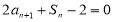 .
.(1)求数列
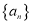 的通项公式.
的通项公式.(2)设
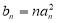 ,求数列
,求数列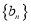 的前
的前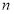 项和
项和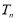 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,下表记录了小李某月1号到5号每天打篮球时间
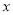 (单位:小时)与当天投篮命中率
(单位:小时)与当天投篮命中率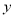 之间的关系:
之间的关系:时间
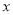
1
2
3
4
5
命中率

0.4
0.5
0.6
0.6
0.4
小李这5天的平均投篮命中率;用线性回归分析的方法,预测小李该月6号打6小时篮球的投篮命中率.
附:线性回归方程
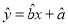 中系数计算公式
中系数计算公式 ,
, 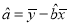 ,
,
相关试题

