【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)当![]() 时,求证:过点
时,求证:过点![]() 有三条直线与曲线
有三条直线与曲线![]() 相切;
相切;
(Ⅱ)当![]() 时,
时,![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(Ⅰ)证明见解析;(Ⅱ)![]() .
.
【解析】试题分析:
(1)![]() ,设直线与曲线
,设直线与曲线![]() 相切,其切点为
相切,其切点为![]() ,求出切线方程,且切线过点
,求出切线方程,且切线过点![]() ,可得
,可得![]() ,判断方程有三个不的根,则结论易得;
,判断方程有三个不的根,则结论易得;
(2) 易得当![]() 时,
时,![]() ,设
,设![]() ,则
,则![]() ,设
,设![]() ,则
,则![]() ,分
,分![]() 、
、![]() 两种情况讨论函数
两种情况讨论函数![]() 的单调性并求出最小值,即可得出结论;
的单调性并求出最小值,即可得出结论;
法二:
(1)同法一得![]() ,设
,设![]() ,求导判断函数的单调性,判断函数的零点个数,即可得出结论;
,求导判断函数的单调性,判断函数的零点个数,即可得出结论;
(2)同法一.
试题解析:
解法一:(Ⅰ)当![]() 时,
时,![]() ,
,
![]()
设直线与曲线![]() 相切,其切点为
相切,其切点为![]() ,
,
则曲线![]() 在点
在点![]() 处的切线方程为:
处的切线方程为:![]() ,
,
因为切线过点![]() ,所以
,所以![]() ,
,
即![]() ,
,
![]() ,
,![]() ,
,
设![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]()
![]() 在三个区间
在三个区间![]() ,
,![]() ,
,![]() 上至少各有一个根
上至少各有一个根
又因为一元三次方程至多有三个根,所以方程![]() 恰有三个根,
恰有三个根,
故过点![]() 有三条直线与曲线
有三条直线与曲线![]() 相切.
相切.
(Ⅱ)![]() 当
当![]() 时,
时,![]() ,即当
,即当![]() 时,
时,![]()
![]() 当
当![]() 时,
时,![]() ,
,
设![]() ,则
,则![]() ,
,
设![]() ,则
,则![]() .
.
(1)当![]() 时,
时,![]() ,从而
,从而![]() (当且仅当
(当且仅当![]() 时,等号成立)
时,等号成立)
![]() 在
在![]() 上单调递增,
上单调递增,
又![]() 当
当![]() 时,
时,![]() ,从而当
,从而当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上单调递减,又
上单调递减,又![]() ,
,
从而当![]() 时,
时,![]() ,即
,即![]()
于是当![]() 时,
时,![]() ,
,
(2)当![]() 时,令
时,令![]() ,得
,得![]()
故当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上单调递减,
上单调递减,
又![]() 当
当![]() 时,
时,![]() ,
,
从而当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上单调递增,又
上单调递增,又![]() ,
,
从而当![]() 时,
时,![]() ,即
,即![]()
于是当![]() 时,
时,![]() ,
,
综合得![]() 的取值范围为
的取值范围为![]() .
.
解法二:(Ⅰ)当![]() 时,
时,![]() ,
,
![]() ,
,
设直线与曲线![]() 相切,其切点为
相切,其切点为![]() ,
,
则曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,
,
因为切线过点![]() ,所以
,所以![]() ,
,
即![]() ,
,
![]() ,
,![]()
设![]() ,则
,则![]() ,令
,令![]() 得
得![]()
当![]() 变化时,
变化时,![]() 变化情况如下表:
变化情况如下表:
![]() 恰有三个根,
恰有三个根,
故过点![]() 有三条直线与曲线
有三条直线与曲线![]() 相切.
相切.
(Ⅱ)同解法一.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数
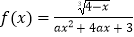 的定义域为(﹣∞,+∞),则实数a的取值范围是( )
的定义域为(﹣∞,+∞),则实数a的取值范围是( )
A.(﹣∞,+∞)
B.[0, )
)
C.( ,+∞)
,+∞)
D.[0, ]
] -
科目: 来源: 题型:
查看答案和解析>>【题目】已知单调递增的等比数列{an}满足:a2+a3+a4=28,且a3+2是a2 , a4的等差中项
①求数列{an}的通项公式;
②设bn=anlog2an , 求数列{bn}的前n项和Sn . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
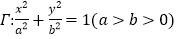 的右焦点
的右焦点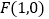 ,椭圆
,椭圆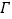 的左,右顶点分别为
的左,右顶点分别为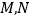 .过点
.过点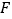 的直线
的直线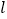 与椭圆交于
与椭圆交于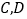 两点,且
两点,且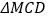 的面积是
的面积是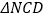 的面积的3倍.
的面积的3倍. (Ⅰ)求椭圆
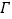 的方程;
的方程;(Ⅱ)若
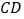 与
与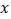 轴垂直,
轴垂直,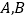 是椭圆
是椭圆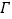 上位于直线
上位于直线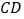 两侧的动点,且满足
两侧的动点,且满足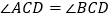 ,试问直线
,试问直线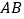 的斜率是否为定值,请说明理由.
的斜率是否为定值,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列函数中既是偶函数又在(﹣∞,0)上是增函数的是( )
A.y=x
B.y=
C.y=x﹣2
D.y=x
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
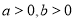 ,函数
,函数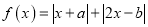 的最小值为1.
的最小值为1.(1)求
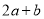 的值;
的值;(2)若
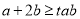 ,求实数
,求实数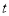 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)当
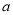 为何值时,
为何值时, 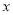 轴为曲线
轴为曲线 的切线;
的切线;(2)用
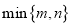 表示
表示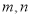 中的最小值,设函数
中的最小值,设函数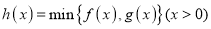 ,讨论
,讨论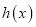 零点的个数.
零点的个数.
相关试题

