【题目】已知函数![]() .
.
(1)当![]() 为何值时,
为何值时, ![]() 轴为曲线
轴为曲线![]() 的切线;
的切线;
(2)用![]() 表示
表示![]() 中的最小值,设函数
中的最小值,设函数![]() ,讨论
,讨论![]() 零点的个数.
零点的个数.
参考答案:
【答案】(1)当![]() 时,
时, ![]() 轴是曲线
轴是曲线![]() 的切线(2)当
的切线(2)当![]() 或
或![]() 时,
时, ![]() 有一个零点;当
有一个零点;当![]() 或
或![]() 时,
时, ![]() 有两个零点;当
有两个零点;当![]() 时,
时, ![]() 有三个零点.
有三个零点.
【解析】【试题分析】(1)先对函数![]() 求导,再运用导数的几何意义建立方程组
求导,再运用导数的几何意义建立方程组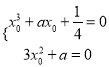 求出
求出![]() ;(2)先确定函数
;(2)先确定函数![]() 的解析表达式的情形,再运用分类整合思想分
的解析表达式的情形,再运用分类整合思想分![]() 或
或![]() 和
和![]() 分类讨论函数
分类讨论函数![]() 的零点的个数问题,进而求出对应的参数的取值范围:
的零点的个数问题,进而求出对应的参数的取值范围:
(1)设曲线![]() 与
与![]() 轴相切于点
轴相切于点![]() ,则
,则![]() ,即
,即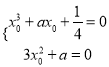 ,
,
解得: ![]() ,
,
因此,当![]() 时,
时, ![]() 轴是曲线
轴是曲线![]() 的切线;
的切线;
(2)当![]() 时,
时, ![]() ,从而
,从而![]() ,
,
∴![]() 在
在![]() 无零点,
无零点,
当![]() 时,若
时,若![]() ,则
,则![]() ,
, ![]() ,故
,故![]() 是
是![]() 的零点; 若
的零点; 若![]() ,则
,则![]() ,
, ![]() ,故
,故![]() 不是
不是![]() 的零点,当
的零点,当![]() 时,
时, ![]() ,所以只需考虑
,所以只需考虑![]() 在
在![]() 的零点个数,
的零点个数,
(Ⅰ)若![]() 或
或![]() ,则
,则![]() 在
在![]() 无零点,故
无零点,故![]() 在
在![]() 单调,而
单调,而![]() ,
,
所以当![]() 时,
时, ![]() 在
在![]() 有一个零点; 当
有一个零点; 当![]() 时,
时, ![]() 在
在![]() 无零点;
无零点;
(Ⅱ)若![]() ,则
,则![]() 在
在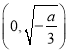 单调递减,在
单调递减,在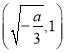 单调递增,
单调递增,
故当![]() 时,
时, ![]() 取的最小值,最小值为
取的最小值,最小值为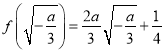 .
.
若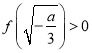 ,即
,即![]() ,
, ![]() 在
在![]() 无零点;
无零点;
若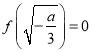 ,即
,即![]() ,则
,则![]() 在
在![]() 有唯一零点;
有唯一零点;
③若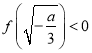 ,即
,即![]() ,由于
,由于![]() ,所以当
,所以当![]() 时,
时, ![]() 在
在![]() 有两个零点;当
有两个零点;当![]() 时,
时, ![]() 在
在![]() 有一个零点.
有一个零点.
综上,当![]() 或
或![]() 时,
时, ![]() 有一个零点;当
有一个零点;当![]() 或
或![]() 时,
时, ![]() 有两个零点;
有两个零点;
当![]() 时,
时, ![]() 有三个零点.
有三个零点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
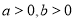 ,函数
,函数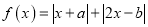 的最小值为1.
的最小值为1.(1)求
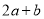 的值;
的值;(2)若
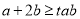 ,求实数
,求实数 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在长方体ABCD﹣A1B1C1D1中,BC=2AB=4,
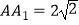 ,E是A1D1的中点.
,E是A1D1的中点.
(Ⅰ)在平面A1B1C1D1内,请作出过点E与CE垂直的直线l,并证明l⊥CE;
(Ⅱ)设(Ⅰ)中所作直线l与CE确定的平面为α,求点C1到平面α的距离.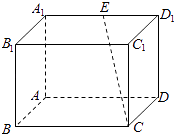
-
科目: 来源: 题型:
查看答案和解析>>【题目】设f(x)是定义在R上的奇函数,且当x≥0时,f(x)=x2 , 若对任意的x∈[t,t+2],不等式f(x+t)≥2f(x)恒成立,则实数t的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义域为R的奇函数f(x)=
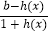 ,其中h(x)是指数函数,且h(2)=4.
,其中h(x)是指数函数,且h(2)=4.
(1)求函数f(x)的解析式;
(2)求不等式f(2x﹣1)>f(x+1)的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,DE∥BC,BC=2DE,CA⊥CB,CA⊥CD,CB⊥CD,F、G分别是AC、BC中点.

(1)求证:平面DFG∥平面ABE;
(2)若AC=2BC=2CD=4,求二面角E﹣AB﹣C的正切值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知公差d>0的等差数列{an}中,a1=10,且a1 , 2a2+2,5a3成等比数列.
(1)求公差d及通项an;
(2)设Sn= +
+  +…+
+…+  ,求证:Sn<
,求证:Sn<  .
.
相关试题

